HannaMadd
- 3
- 0
Hi everyone!
I have perhaps a basic question, but I can't dealt with it.
I have a rectangular sample 50x150mm of let's say wood. The sample is compressed from the top over the width of 4mm. I know the shortening of the sample at 70 mm from the bottom (from experimental testing) and I know the force. The shortening is 0.2mm. But I need to know how much the sample shortens at the top, assuming triangle stress distribution. This is a 2D problem. Please, take a look at the sketch.
Thank you for any suggestions!
Hana
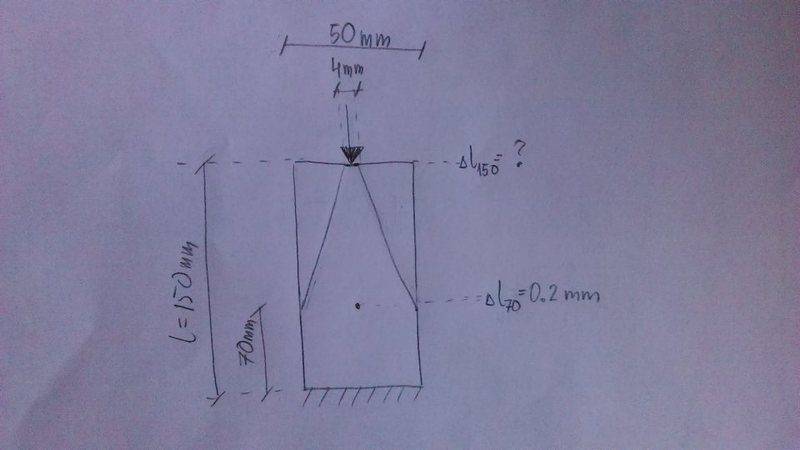
I have perhaps a basic question, but I can't dealt with it.
I have a rectangular sample 50x150mm of let's say wood. The sample is compressed from the top over the width of 4mm. I know the shortening of the sample at 70 mm from the bottom (from experimental testing) and I know the force. The shortening is 0.2mm. But I need to know how much the sample shortens at the top, assuming triangle stress distribution. This is a 2D problem. Please, take a look at the sketch.
Thank you for any suggestions!
Hana