pcmarine
- 6
- 0
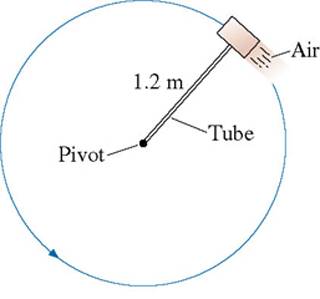
A 600 g steel block rotates on a steel table while attached to a 1.20 m-long hollow tube. Compressed air fed through the tube and ejected from a nozzle on the back of the block exerts a thrust force of 4.30 N perpendicular to the tube. The maximum tension the tube can withstand without breaking is 60.0 N.
If the block starts from rest, how many revolutions does it make before the tube breaks?
I've done some calculations and have come up with:
Tangential Acceleration: 1.287 m/s^2
Omega: 9.13
Period: 8.513 seconds
plugged these numbers into Theta=((a)/(2*r))*(period)^2
and got 38.953 rads, or 61.19 revolutions... which was wrong
If the block starts from rest, how many revolutions does it make before the tube breaks?
I've done some calculations and have come up with:
Tangential Acceleration: 1.287 m/s^2
Omega: 9.13
Period: 8.513 seconds
plugged these numbers into Theta=((a)/(2*r))*(period)^2
and got 38.953 rads, or 61.19 revolutions... which was wrong