A Normalization and Scaling with Matrices

[doublee89]

Hey everyone, I understand how to normalize a second order system, but I wanted to know if the same steps are taken when the parameters of the system are not scalar but matrices. For example

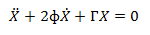
where the parameter phi, and gamma are both 3x3 matrices and X is a 3x1 vector.

From what I've see online it doesn't look like it's the same when matrices are involved, and I can't seem to even find a textbook that will walk me through this step by step.

Any ideas?

 

[Stephen Tashi]

Hey everyone, I understand how to normalize a second order system,

What kind of "normalization" are we going to do ? In some contexts, the term "normalize" means to put a differential equation into dimensionless form.

 

[SPFF]

That is exactly the kind of normalization I was hoping for. Also, I know that in the scalar case normalizing the differential equation can reduce the number of parameters (which would also be a plus) but more than anything else I care about producing dimensionless and scaled parameters. The scaling is important to me because I will be putting this differential equation in state space form. The resulting dynamics matrix is poorly conditioned for some values and I would like to improve the condition number in the general case. This normalization/scaling could help with that.

 

[Stephen Tashi]

That is exactly the kind of normalization I was hoping for.

I'm confused. Are you working the same problem as @doublee89 ?

 

[SPFF]

That was me (doublee89).. I am not sure why my account name has been changed. Strange...

 

[Stephen Tashi]

Perhaps you browser saved the wrong user name and password for auto-login.

I don't know of any way to specify an algorithm to "nondimensionalize" a system of simultaneous differential equations.

Your matrix differential equation is equivalent to 3 simultaneous differential equations. The steps to "nondimensionalize" a single differential equation involve substituting a constant times a new variable for an old variable and dividing the equation by constants. Working with a system of equations, when we substitute a new variable for an old one, we can do it in all the equations. We can divide anyone of the equations by a constant.

The new possibility that a system of equations introduces is that we can replace an equation by a linear combination of other equations. It isn't clear to me whether changing variables creates any possibilities for simplifying the system of equations though using linear combinations that weren't already there in the original equations.

I agree that it's hard to find examples of nondimensionalizing a system of equations on the web. I did find this example of nondimensionalizing the two differential equations for a predator-prey system: https://daphnia.ecology.uga.edu/ceesg/wp-content/uploads/2014/01/nondim_notes.pdf