Recipi
- 6
- 0
Odd Form Of Eigenvalue -- Coupled Masses
This isn't strictly homework, since it's something I'm trying to self-teach, but it seems to fit best here.
It's an example of applying eigenvalue methods to solve (classical) mechanical systems in an introductory text to QM; specifically, 1.8.6 in Shankar. I can follow everything fine until it actually comes to calculating the eigenvalues; when I tried to do it without looking at the result, mine was out by a sign and square root.
The exact text is "...the eigenvalue of Ω is written as -ω^2 rather than ω in anticipation of the fact that Ω has eigenvalues of the form -ω^2, with ω real". How quickly it's glossed over makes me think I'm missing something obvious, but I can't for the life of me see it. I've reproduced my work up to that point below.
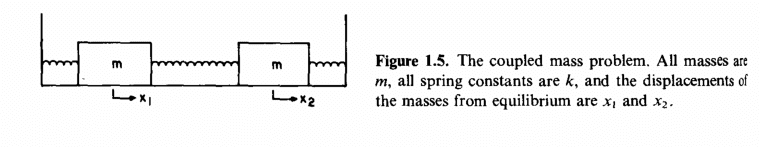
"Determine x_1(t) and x_2(t) given the initial displacements x_1(0) and x_2(0) and that both masses are initially at rest."
Applying Hooke's law and F=ma:
<br /> \\<br /> {x}_1'' = -\frac{2k}{m}x + \frac{k}{m}x \\<br /> {x}_2'' = \frac{k}{m}x_1 - 2\frac{k}{m}x_2 \\ \\<br /> \varkappa \equiv \frac{k}{m} \\<br /> \begin{bmatrix}<br /> {x}_1''\\ <br /> {x}_2''<br /> \end{bmatrix} = \begin{bmatrix}<br /> -2\varkappa & \varkappa \\ <br /> \varkappa & -2\varkappa<br /> \end{bmatrix}\begin{bmatrix}<br /> x_1\\ <br /> x_2<br /> \end{bmatrix} \\<br /> \left|x''(t)\right\rangle= \Omega \left|x(t)\right\rangle<br />
This is in the basis with one vector equal to a unit displacement of the first mass, and the other the same for the second; the coupled differential equation is a pain to solve, so I want to swap to a basis with no contribution from x_1 to x_2 and vice versa, so diagonalising the Hermitian Ω as usual (det(Ω - ωI) = 0 and making a unitary diagonalising matrix from the eigenvector components) I end up with \omega_1 = -\varkappa and \omega_2 = -3\varkappa. The book itself gets \omega_1 = \sqrt{\varkappa} and \omega_2 = \sqrt{3\varkappa}, which fits with the assumed form of ω, but I don't know where that comes from.
Sorry if this is too much information, since a lot of it seems ancillary to the question of "Why is the eigenvalue taken to be that form?", but I wanted to err on the side of caution with my first post.
This isn't strictly homework, since it's something I'm trying to self-teach, but it seems to fit best here.
Homework Statement
It's an example of applying eigenvalue methods to solve (classical) mechanical systems in an introductory text to QM; specifically, 1.8.6 in Shankar. I can follow everything fine until it actually comes to calculating the eigenvalues; when I tried to do it without looking at the result, mine was out by a sign and square root.
The exact text is "...the eigenvalue of Ω is written as -ω^2 rather than ω in anticipation of the fact that Ω has eigenvalues of the form -ω^2, with ω real". How quickly it's glossed over makes me think I'm missing something obvious, but I can't for the life of me see it. I've reproduced my work up to that point below.
Homework Equations
&The Attempt at a Solution
"Determine x_1(t) and x_2(t) given the initial displacements x_1(0) and x_2(0) and that both masses are initially at rest."
Applying Hooke's law and F=ma:
<br /> \\<br /> {x}_1'' = -\frac{2k}{m}x + \frac{k}{m}x \\<br /> {x}_2'' = \frac{k}{m}x_1 - 2\frac{k}{m}x_2 \\ \\<br /> \varkappa \equiv \frac{k}{m} \\<br /> \begin{bmatrix}<br /> {x}_1''\\ <br /> {x}_2''<br /> \end{bmatrix} = \begin{bmatrix}<br /> -2\varkappa & \varkappa \\ <br /> \varkappa & -2\varkappa<br /> \end{bmatrix}\begin{bmatrix}<br /> x_1\\ <br /> x_2<br /> \end{bmatrix} \\<br /> \left|x''(t)\right\rangle= \Omega \left|x(t)\right\rangle<br />
This is in the basis with one vector equal to a unit displacement of the first mass, and the other the same for the second; the coupled differential equation is a pain to solve, so I want to swap to a basis with no contribution from x_1 to x_2 and vice versa, so diagonalising the Hermitian Ω as usual (det(Ω - ωI) = 0 and making a unitary diagonalising matrix from the eigenvector components) I end up with \omega_1 = -\varkappa and \omega_2 = -3\varkappa. The book itself gets \omega_1 = \sqrt{\varkappa} and \omega_2 = \sqrt{3\varkappa}, which fits with the assumed form of ω, but I don't know where that comes from.
Sorry if this is too much information, since a lot of it seems ancillary to the question of "Why is the eigenvalue taken to be that form?", but I wanted to err on the side of caution with my first post.