etf
- 179
- 2
Hi!
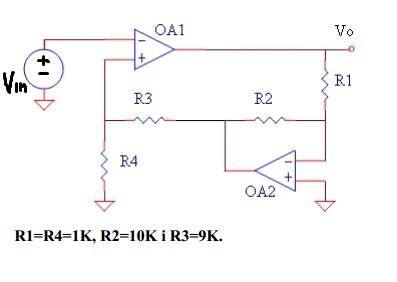
My task is to calculate gain A=Vo/Vin for circuit on scheme (OPAMPS are ideal):
Since OPAMPS are ideal, input currents are zero and V1=V2=Vin, V11=V22=0:
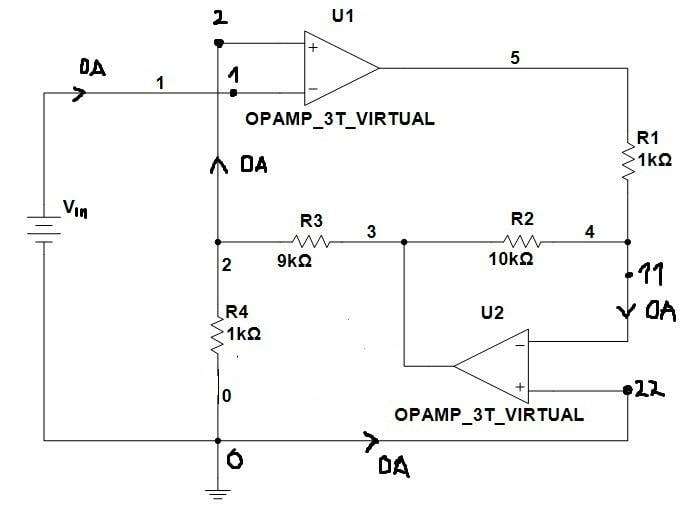
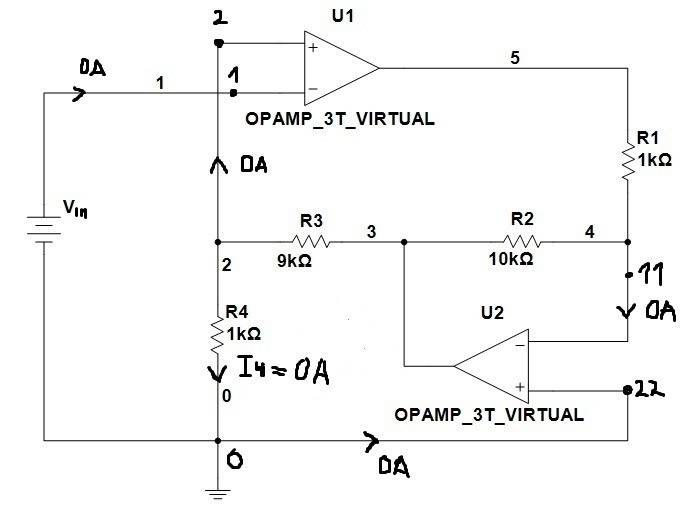
KCL for node 0 suggests us that current through R4 (I4) must be zero:
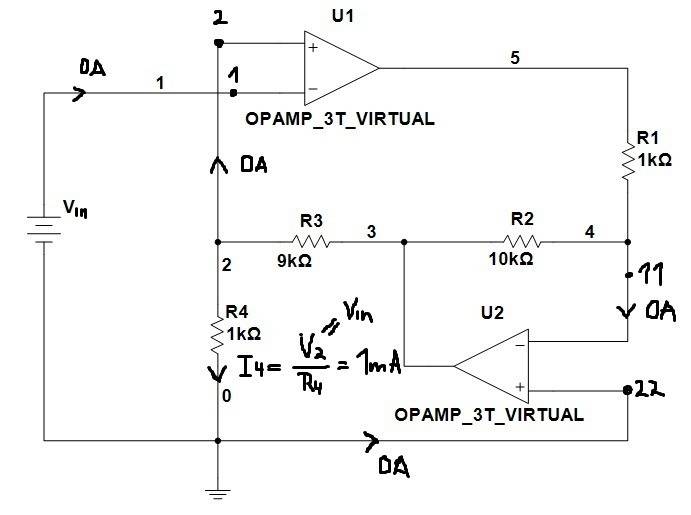
On the other hand, we can calculate I4 as:



I tested circuit using Multisim and I got this:
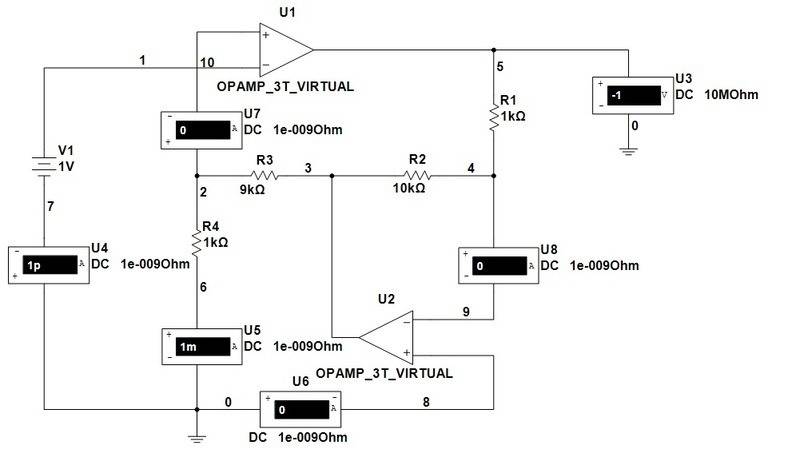
For any input voltage Vin we have on output Vo=-Vin
My task is to calculate gain A=Vo/Vin for circuit on scheme (OPAMPS are ideal):
Since OPAMPS are ideal, input currents are zero and V1=V2=Vin, V11=V22=0:
KCL for node 0 suggests us that current through R4 (I4) must be zero:
On the other hand, we can calculate I4 as:
I tested circuit using Multisim and I got this:
For any input voltage Vin we have on output Vo=-Vin