- #1
Cynosura
- 5
- 0
So, I'm about to take an Optics exam, and while I can easily do most of the last years' exam problems, there are some which I cannot solve for different reasons (perhaps some gross oversight?). Yesterday I stumbled upon this:
1. Homework Statement
(my own translation from Catalan)
We have a rectangular prism with an small angle of α=0.1 rad and an index of refraction n=1.5 at distance d=20 mm to the right of a point source emitting at λ0=500 nm. 1m to the right of the prism lies a screen, as seen in the drawing.
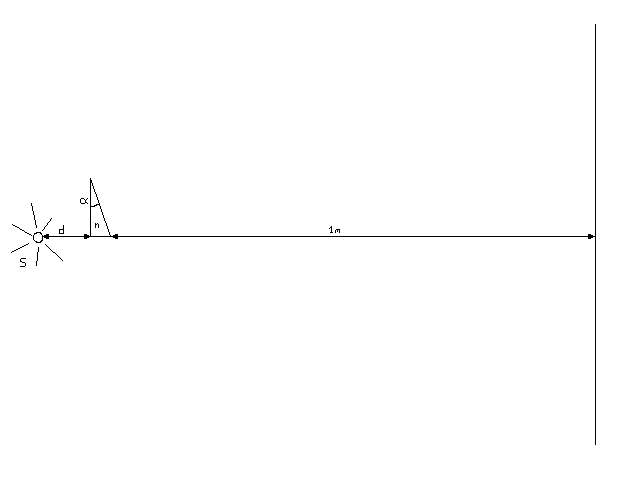
(had to draw it myself, it wouldn't let me use the original image)
a) Calculate the angle of deviation of a light beam in normal incidence.
b) Draw where on the screen will be interference fringes, and calculate the width of the zone in which they can be observed.
c) Calculate the separation between two consecutive fringes.
d) How many minima and maxima can be observed?
Two-beam interference, Snell's law.
a) I applied Snell's law on the second surface of the prism, since a prependicular surface does not refract light. It gave me an angle between the axis and the beam (which I will call β) of 0.05032 radians.
b) The interference zone will lie between the axis (since above it there is only one incident beam and the point where the normally incident beam strikes the screen. To calculate that, I applied the definition of the tangent of an angle, and obtained that the lowermost point on the screen where fringes may be observed is x=50.36 mm. But I cannot solve the uppermost point, since it seems to depend on the size of the prism (which is not there!). I could slap "let's assume that the prism is big enough so that there is incident light just above the axis" in there, but I've gotten bad marks for that type of thing before, or I could try and calculate the height of that point as a function of one of the prism's dimensions, but that looks downright nasty having in mind the timeframe of an exam. Did I miss something?
c) My sketch here consists of finding the point where two beams from the prism cross, use that as a second source and apply the equation that s·sin(θ)=mλ, where s is the separation between sources, θ is the angle between the point we are evaluating and the rect which is always equidistant to both sources, and m is an integer. I have not plugged the values yet because I'm doubtful of my assumptions being sensible.
d) I cannot solve it because it depends on b).Any measure of help will be greatly appreciated.
1. Homework Statement
(my own translation from Catalan)
We have a rectangular prism with an small angle of α=0.1 rad and an index of refraction n=1.5 at distance d=20 mm to the right of a point source emitting at λ0=500 nm. 1m to the right of the prism lies a screen, as seen in the drawing.
(had to draw it myself, it wouldn't let me use the original image)
a) Calculate the angle of deviation of a light beam in normal incidence.
b) Draw where on the screen will be interference fringes, and calculate the width of the zone in which they can be observed.
c) Calculate the separation between two consecutive fringes.
d) How many minima and maxima can be observed?
Homework Equations
Two-beam interference, Snell's law.
The Attempt at a Solution
a) I applied Snell's law on the second surface of the prism, since a prependicular surface does not refract light. It gave me an angle between the axis and the beam (which I will call β) of 0.05032 radians.
b) The interference zone will lie between the axis (since above it there is only one incident beam and the point where the normally incident beam strikes the screen. To calculate that, I applied the definition of the tangent of an angle, and obtained that the lowermost point on the screen where fringes may be observed is x=50.36 mm. But I cannot solve the uppermost point, since it seems to depend on the size of the prism (which is not there!). I could slap "let's assume that the prism is big enough so that there is incident light just above the axis" in there, but I've gotten bad marks for that type of thing before, or I could try and calculate the height of that point as a function of one of the prism's dimensions, but that looks downright nasty having in mind the timeframe of an exam. Did I miss something?
c) My sketch here consists of finding the point where two beams from the prism cross, use that as a second source and apply the equation that s·sin(θ)=mλ, where s is the separation between sources, θ is the angle between the point we are evaluating and the rect which is always equidistant to both sources, and m is an integer. I have not plugged the values yet because I'm doubtful of my assumptions being sensible.
d) I cannot solve it because it depends on b).Any measure of help will be greatly appreciated.