vishwesh
- 10
- 0
Homework Statement
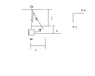
A mass m hangs on a spring of constant k. In the position of static equilibrium the length of the spring is l. If the mass is drawn sideways and then released,the ensuing motion will be a combination of (a) pendulum swings and (b) extension and compression of the spring. Without using a lot of mathematics, consider the behavior of this arrangement as a coupled system.
I have attached the figure I drew for this problem.
Homework Equations
The Attempt at a Solution
For x - direction:
## m \cfrac{d^2 x}{d t^2} + m {\omega_{0}}^2 x = 0 ##
##\implies \cfrac{d^2 x}{d t^2} + {\omega_{0}}^2 x = 0 \tag{1} ##
##\implies \cfrac{d^2 x}{dt^2} + \cfrac{g}{l} x = 0\tag{1}##
For y - direction:
## m \cfrac {d^2 y}{d t^2} + ky = mg ##
##\implies \cfrac{d^2 y}{d t^2} + \cfrac{k}{m} y = g \tag{2}##Solution for equation (1) would be:
## x = A \cos (\omega_{0} t) \tag{3}##
Solution for equation (2) would be:
##y = B \cos (\omega t) \tag{4}##
Am I on the right track and how should I proceed?
Thanks
Attachments
Last edited: