Paradox of a convergent nozzle fed by an electric fan

[eudesvera3]

Let us assume we have a cylindrical wind tunnel having a 0.5 m diameter fed by an electric fan. The cross-sectional area of the wind tunnel would be A1 = (PI/4) D1^2 = 0.196349541 m2. Let us suppose the motor driving the fan has a power rating of 1,500 W. At this stage, let us assume that the electric motor is consuming its maximum power rating, and that the measured airflow velocity is V1 = 20 m/s, just at the output of the wind tunnel. The kinetic power P1 of the airflow just at the output of the wind tunnel can be calculated as by applying the formula P1 = (1/2) (density of air) (A1) (V1^3) = 962.11 W. If we viewed the wind tunnel plus the fan and the electric motor as a system (System 1), we could say that the efficiency of this system 1 would be System 1 Efficiency = 100 P1/1500 = 64.14%.

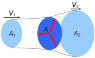
At this stage, let us consider a new system (System 2), formed by system 1 plus a 2:1 ratio convergent nozzle attached to the output of system 1. Now the output of system 2 would have a cross-sectional area A2 given by A2 = 0.09817477 m2. If now the electric motor is ran at its maximum power rating as before, can we expect the velocity of the airflow just at the output of the convergent nozzle to be V2 = 40 m/s?

If that were the case, the kinetic power P2 of of the airflow just at the output of the convergent nozzle would be P2 = (1/2) (density of air) (A2) (V2^3) = 3,848.45 W. Notice that now the power of the output airflow would be greater than the input power to the system (1, 500 W), which would apparently be a violation of first law of thermodynamics. Moreover, the efficiency of system 2 would be System 2 Efficiency = 100 P2/1500 = 256.56%, which apparently constitute a violation of second law of thermodynamics also.
Is there a flaw in this analysis?

 

[russ_watters]

At this stage, let us assume that the electric motor is consuming its maximum power rating, and that the measured airflow velocity is V1 = 20 m/s, just at the output of the wind tunnel...

At this stage, let us consider a new system (System 2), formed by system 1 plus a 2:1 ratio convergent nozzle attached to the output of system 1. Now the output of system 2 would have a cross-sectional area A2 given by A2 = 0.09817477 m2. If now the electric motor is ran at its maximum power rating as before, can we expect the velocity of the airflow just at the output of the convergent nozzle to be V2 = 40 m/s?...

Is there a flaw in this analysis?

Welcome to PF.

The flaw is that you didn't do any real analysis of the fan's performance; you just multiplied the outlet velocity by 2!

Real fans have performance curves that must be used to analyze the fan's performance when attached to a given system.

 

[.Scott]

The nozzle will create back pressure on the fan - and that will slow the airflow and the fan.

 

[eudesvera3]

Welcome to PF.

The flaw is that you didn't do any real analysis of the fan's performance; you just multiplied the outlet velocity by 2!

Real fans have performance curves that must be used to analyze the fan's performance when attached to a given system.

Thank you russ_waters. You are certainly right, I did not actually do any real analysis of the fan's performance. Sorry about that. However I just wanted to point out the issue whether it was possible at all that a system formed by an electric fan, a wind tunnel and a convergent nozzle could produce an airflow power greater than the motor power. But your opinion is certainly very valuable to me.

 

[eudesvera3]

The nozzle will create back pressure on the fan - and that will slow the airflow and the fan.

Scott, I appreciate very much your opinion. It seems very reasonable to me that the back pressure on the fan will not allow the airflow power to go beyond the motor power. In other words an output airflow velocity of 40 m/s would never be possible in this particular system and hence no violation of thermodynamic laws could occur.

 

[Dale]

If now the electric motor is ran at its maximum power rating as before, can we expect the velocity of the airflow just at the output of the convergent nozzle to be V2 = 40 m/s?

Clearly not, as your subsequent analysis shows.

Is there a flaw in this analysis?

Yes, the non physical assumption that a nozzle increases the power of a fluid flow.

 

[eudesvera3]

Clearly not, as your subsequent analysis shows.

Yes, the non physical assumption that a nozzle increases the power of a fluid flow.

Well, the purpose of my post was to learn from your opinions and to try to clarify this apparent paradox, because I am sure you will admit that in the case there was not an artificial airflow but a wind flow as it happens in the Invelox wind turbine, if the velocity of the wind flow at the entrance of a 2:1 ratio convergent nozzle is 20 m/s, then the velocity at the output of the CN will be 40 m/s, and the output wind power would be 4 times the wind power at the entrance of the CN. So the convergent nozzle in this case does increase the power of the wind flow. Thank you for your most valuable opinion.

 

[Dale]

if the velocity of the wind flow at the entrance of a 2:1 ratio convergent nozzle is 20 m/s, then the velocity at the output of the CN will be 40 m/s,

Assuming an incompressible flow that is always the case. But that does not mean that your conclusion follows.

I will post details later

 

[russ_watters]

Well, the purpose of my post was to learn from your opinions and to try to clarify this apparent paradox, because I am sure you will admit that in the case there was not an artificial airflow but a wind flow as it happens in the Invelox wind turbine, if the velocity of the wind flow at the entrance of a 2:1 ratio convergent nozzle is 20 m/s, then the velocity at the output of the CN will be 40 m/s...

That's true, but do you see the difference between this and the scenario you first proposed?

...and the output wind power would be 4 times the wind power at the entrance of the CN.

That isn't true. You are neglecting to account for pressure. Conservation of energy applies. This is the point of Bernoulli's principle.

Pro tip: if you are ever not sure if conservation of energy applies, the answer is that it does apply.

 

[eudesvera3]

That's true, but do you see the difference between this and the scenario you first proposed?

That isn't true. You are neglecting to account for pressure. Conservation of energy applies. This is the point of Bernoulli's principle.

Pro tip: if you are ever not sure if conservation of energy applies, the answer is that it does apply.

I agree, conservation of energy always apply. But within the nozzle the increase of kinetic energy at the narrower end of the nozzles comes about at the expense of a reduction of the enthalpy of the flow at that end in such a way that the total energy at that end is exactly the same as the total energy at the entrance of the nozzle. So energy conservation is kept within the nozzle as it should outside. However, how do you reconcile the apparent fact that the power of the airflow coming out of the narrow end at 40 m/s is 4 times the power of the airflow coming into the wide end at 20 m/s? There seems to be an incongruence here, but the only explanation I can find here is that the total energy entering the nozzle is composed of kinetic energy and thermal plus pressure energy (enthalpy), and the sum of these two must be preserved at all times. Nevertheless, the kinetic energy does not require preservation, Thus it is perfectly possible for the kinetic power at the output of the nozzle to be 4 times greater than the kinetic power at the input of the nozzle, and that would not constitute a violation of conservation of energy on account of the fact that the thermal energy (or more exactly, the enthalpy) of the airflow is reduced (i.e., a drop in temperature and pressure takes place in the very exact amount as the kinetic energy increases. So I contend unless I am proven wrong that the kinetic power at the output of a 2:1 ratio convergent nozzle is 4 times greater than the kinetic power at the entrance of the CN. Thank you for your opinion and for reading my post.

 

[Dale]

However, how do you reconcile the apparent fact that the power of the airflow coming out of the narrow end at 40 m/s is 4 times the power of the airflow coming into the wide end at 20 m/s?

The power of the airflow at the exit is not 4 times the power at the inlet. That is where you are going wrong. The KE is 4 times greater, but the hydraulic energy (pressure * volume) is reduced.

As @russ_watters mentioned, this is covered by Bernoulli’s principle. For an incompressible horizontal flow any increase in $\frac{1}{2}\rho v^2$ is accompanied by an equal decrease in $p$. So the total energy is unchanged, as it must be by a device that does no work.

kinetic power at the output of a 2:1 ratio convergent nozzle is 4 times greater

The term “kinetic power” is not one that I have heard before, but assuming that it means what I think it means then “kinetic power” is not the same as “power”. So the above objections stand as worded, but similar statements specifying “kinetic power” would be non controversial beyond possible semantic objections. Certainly it is no paradox.

 

[eudesvera3]

The power of the airflow at the exit is not 4 times the power at the inlet. That is where you are going wrong. The KE is 4 times greater, but the hydraulic energy (pressure * volume) is reduced.

As @russ_watters mentioned, this is covered by Bernoulli’s principle. For an incompressible horizontal flow any increase in $\frac{1}{2}\rho v^2$ is accompanied by an equal decrease in $p$. So the total energy is unchanged, as it must be by a device that does no work.

The term “kinetic power” is not one that I have heard before, but assuming that it means what I think it means then “kinetic power” is not the same as “power”. So the above objections stand as worded, but similar statements specifying “kinetic power” would be non controversial beyond possible semantic objections. Certainly it is no paradox.

Thank you for clearing this up for me. Probably I did not express myself very well. What I meant to say was precisely what you has just pointed out, i.e., that the KE at the exit is 4 times greater than the KE at the inlet.

Regarding the term "kinetic power", I am sorry for my poor choosing of words as I am still in the learning process of the English language. What I meant to say was that the rate of change of KE at the exit is 4 times the rate of change of KE at the inlet. Since these two physical quantities I believe are measured in Watts hence the use of the term kinetic power to describe them.

Now, going back to the system formed by the electric motor, the fan, the wind tunnel and the 2:1 ratio convergence nozzle I wonder if the power contained in the KE of the airflow at the exit could be greater than the motor power. Scott has already said that is not possible because of the increase in pressure that takes place on the fan blades and reduces the airflow velocity. Kindly could you give me your opinion about that?

 

[Dale]

I wonder if the power contained in the KE of the airflow at the exit could be greater than the motor power.

No (obviously). This is a direct result of Bernoulli’s principle, which is simply conservation of energy.

Scott has already said that is not possible because of the increase in pressure that takes place on the fan blades and reduces the airflow velocity. Kindly could you give me your opinion about that?

Both @.Scott and @russ_watters are correct. You can use Bernoulli’s principle to calculate the pressure at the inlet of the nozzle and from thence the energy required by the fan.

 

[russ_watters]

@eudesvera3 please read about Bernoulli's Principle: https://en.wikipedia.org/wiki/Bernoulli's_principle

 

[eudesvera3]

No (obviously). This is a direct result of Bernoulli’s principle, which is simply conservation of energy.

Both @.Scott and @russ_watters are correct. You can use Bernoulli’s principle to calculate the pressure at the inlet of the nozzle and from thence the energy required by the fan.

I am most grateful to you for your prompt and clear response. Now I can see there is no paradox at all.

 

[eudesvera3]

@eudesvera3 please read about Bernoulli's Principle: https://en.wikipedia.org/wiki/Bernoulli's_principle

Thanks for the suggestion. I think I understand Bernoulli's principle. It's just that for any given motor power the airflow velocity at the inlet of a convergent nozzle can not be arbitrarily assumed as I was wrongly doing. If this airflow velocity is arbitrarily assumed then the airflow velocity at the nozzle exit can be wrongly calculated although Bernoulli's equation is properly used.

 

[russ_watters]

As best as I can tell, this is a scenario like the OP describes. Here is a random fan curve:

If not connected to a system, the fan is allowed to free-blow, and the fan curve tells us the airflow is 2550 CFM, or a velocity of 3072 fpm.

However, the outlet velocity in the selected configuration is 1802 fpm (1550 CFM) and the static pressure 4.0" w.g. Velocity pressure is often ignored when it is a small fraction of static pressure, but in this case it is 0.2". If the only thing attached to this fan is a nozzle, a nozzle ratio of 4.55:1 will provide a final velocity of 8208 fpm, using up all that 4.2" of available total pressure (outlet static pressure is 0/atmospheric).

• This is how Bernoulli's principle/the Venturi effect works, for incompressible flow, with no losses.
• This is how real fans work.

Note, @.Scott in this case the fan is turned by a 3-phase motor and the rpm is fixed. For some motors/fans, the rpm will drop if you add a nozzle, as you said.

 

[russ_watters]

Off topic posts have been split to this thread:
https://www.physicsforums.com/threads/bernoullis-principle-and-fans-split.954738/

 

[eudesvera3]

We were discussing incompressible flows here. This is a reasonable approximation for low Mach numbers, and here we are dealing with around Mach 0.1, so the incompressible flow is a good assumption.

I don’t believe this. Please cite the scientific reference that you believe teaches this.

If I may, I would like to try to reach some conclusions for this thread, and please correct me if I am wrong.

Conclusion 1. When a convergent nozzle is attached to a fan driven by an electric motor it is impossible due to the back pressure generated by the nozzle for the kinetic power of the airflow at the nozzle exit to be greater than the motor power.

Conclusion 2. If a convergent nozzle is used to accelerate wind before applying it to a wind turbine, the kinetic power of the wind flow at the exit of the nozzle will always be greater than the kinetic power of the wind flow at the inlet of the nozzle. As an example, if a 2:1 ratio convergence nozzle is used, the outlet kinetic power will be exactly 4 times greater than the inlet kinetic power.

For both conclusions, it is assumed that the flow is inviscid, incompressible, steady and horizontal. In addition, by kinetic power it is meant the following physical quantity:(1/2) times (cross-sectional area seen by airflow) times (velocity of the airflow at such area to the cubic power). In other words, kinetic power of a flow is simply its kinetic energy per unit time.

 

[Dale]

Looks good to me, although I didn’t check the math on that last part.

 

[eudesvera3]

Looks good to me, although I didn’t check the math on that last part.

Thank you Dale. I feel rewarded with a better understanding of convergent nozzles thanks to your contribution to the discussion and that of the other participants. It is a shame that convergent nozzles do not seem to be very productive for raising airflow speed without increasing back pressure on the fan. If that difficulty could be sorted out somehow, then convergent nozzles would be a great help to increase airflow velocity.

On the other hand, the usefulness of convergent nozzles for increasing the power generated by wind turbines seem to be out of question, although they also increase the drag power. Nevertheless, since current augmented wind turbines can not exceed the theoretical Jamieson's limit on efficiency (88.89%), convergent nozzles can do nothing to improve this efficiency, unless some modification of these turbines can be made, but this has not occurred yet, to the best of my knowledge. Perhaps the research team to which I belong could suggest something soon in this respect.

 

[russ_watters]

If I may, I would like to try to reach some conclusions for this thread, and please correct me if I am wrong.

Conclusion 1. When a convergent nozzle is attached to a fan driven by an electric motor it is impossible due to the back pressure generated by the nozzle for the kinetic power of the airflow at the nozzle exit to be greater than the motor power.

Conclusion 2. If a convergent nozzle is used to accelerate wind before applying it to a wind turbine, the kinetic power of the wind flow at the exit of the nozzle will always be greater than the kinetic power of the wind flow at the inlet of the nozzle. As an example, if a 2:1 ratio convergence nozzle is used, the outlet kinetic power will be exactly 4 times greater than the inlet kinetic power.

These are correct, though I want to add a quick caveat to make sure about a critical issue with #2, since you didn't acknowledge it before: While the kinetic energy is 4x greater at the outlet than inlet, that should not be construed to believe the inlet kinetic energy is equal to a situation where there nozzle wasn't there to begin with. In other words, the inlet kinetic energy is lower with the nozzle in place than without it.

...your next post seems to imply you understand that, but I wanted to make it clear.

For both conclusions, it is assumed that the flow is inviscid, incompressible, steady and horizontal. In addition, by kinetic power it is meant the following physical quantity:(1/2) times (cross-sectional area seen by airflow) times (velocity of the airflow at such area to the cubic power). In other words, kinetic power of a flow is simply its kinetic energy per unit time.

Looks like you just forgot the density of the air, but otherwise ok.

 

[eudesvera3]

These are correct, though I want to add a quick caveat to make sure about a critical issue with #2, since you didn't acknowledge it before: While the kinetic energy is 4x greater at the outlet than inlet, that should not be construed to believe the inlet kinetic energy is equal to a situation where there nozzle wasn't there to begin with. In other words, the inlet kinetic energy is lower with the nozzle in place than without it.

...your next post seems to imply you understand that, but I wanted to make it clear.

Looks like you just forgot the density of the air, but otherwise ok.

These are correct, though I want to add a quick caveat to make sure about a critical issue with #2, since you didn't acknowledge it before: While the kinetic energy is 4x greater at the outlet than inlet, that should not be construed to believe the inlet kinetic energy is equal to a situation where there nozzle wasn't there to begin with. In other words, the inlet kinetic energy is lower with the nozzle in place than without it.

...your next post seems to imply you understand that, but I wanted to make it clear.

Looks like you just forgot the density of the air, but otherwise ok.

Right, I forgot the density of air, which is very important. Now, regarding your caveat I find most interesting your comment that the inlet kinetic energy is lower with the nozzle in place than without it and I wonder if that is due to the drag although small introduced by the nozzle. If that is the case, the difference between both energies should not be large, I think, and the introduction of the nozzle will certainly be advantageous and advisable. I also wonder if there is a limitation as to the maximum area ratio the convergent nozzle should have. I would dare to say that the only limitation on this ratio should not be other than keeping the airflow velocity under 0.3 Mach.

Another aspect I would like your opinion on is regarding the maximum nozzle slope that is suitable to use with wind turbines if we aim to reduce the length of the whole system. Thanks in advance.

 

[russ_watters]

Right, I forgot the density of air, which is very important. Now, regarding your caveat I find most interesting your comment that the inlet kinetic energy is lower with the nozzle in place than without it and I wonder if that is due to the drag although small introduced by the nozzle. If that is the case, the difference between both energies should not be large, I think, and the introduction of the nozzle will certainly be advantageous and advisable.

It's because the added back pressure causes air to spill out around the funnel instead of going through it. And for a wind turbine, since wind has no static pressure to convert to kinetic energy, conservation of energy demands that the funnel won't help at all.

 

[eudesvera3]

It's because the added back pressure causes air to spill out around the funnel instead of going through it. And for a wind turbine, since wind has no static pressure to convert to kinetic energy, conservation of energy demands that the funnel won't help at all.

So, according to your appreciation, the use of a funnel in wind turbines like Sheerwind Invelox turbine (, https://www.sciencedirect.com/science/article/pii/S0360544214002837) is just baloney? And would you please explain why the wind do not have static pressure, despite being a fluid? Is it because it is not a steady flow?

 

[russ_watters]

So, according to your appreciation, the use of a funnel in wind turbines like Sheerwind Invelox turbine (, https://www.sciencedirect.com/science/article/pii/S0360544214002837) is just baloney?

I wouldn't say baloney necessarily. What it does is allow for a smaller turbine, at the expense of the funnel. I doubt it's an economically viable trade off.

...they are also claiming a benefit from being omnidirectional.

 

[eudesvera3]

I wouldn't say baloney necessarily. What it does is allow for a smaller turbine, at the expense of the funnel. I doubt it's an economically viable trade off.

...they are also claiming a benefit from being omnidirectional.

Thanks for clarifying. I do like its omni directional feature and the ease of maintenance at ground level plus the use of a funnel Another advantage is the possibility of feeding several turbines with the same wind flow. However, there have been several criticism of this turbine (https://cleantechnica.com/2014/07/08/invelox-ducted-turbine-latest-long-line-failures/,, https://www.technologyreview.com/s/508136/ducted-wind-turbines-an-energy-game-changer/). Notwithstanding, that I think this turbine has potential and room for improvement. But I must say I am puzzled by your assertion that wind has not static pressure which is almost equivalent to say it has no enthalpy, just velocity. So how can Bernoulli equation be written for wind if this fluid does not have static pressure? But, please bear with me and excuse my ignorance in Fluid Mechanics.

 

[russ_watters]

But I must say I am puzzled by your assertion that wind has not static pressure which is almost equivalent to say it has no enthalpy, just velocity. So how can Bernoulli equation be written for wind if this fluid does not have static pressure? But, please bear with me and excuse my ignorance in Fluid Mechanics.

0 gauge pressure. For air in an open duct, the zero reference is atmospheric. For wind, its reference is itself. In Bernoulli's equation it is common to use gauge pressure.

 

[eudesvera3]

Thank you. Can you tell me if I can close this thread and how to do it?

 

[cjl]

One interesting thing that hasn't been mentioned yet. It is possible to end up with a higher flow kinetic energy than the fan power in some specialized setups. Specifically, you could have a fan at the entrance to a nozzle (funnel), which contracts down to a narrow section before then entering a diffuser (funnel pointing the other way) before exhausting to ambient. In this setup, assuming reasonably smooth transitions so as to maximize efficiency of the nozzle and diffuser, the kinetic energy of the flow in the narrow section could indeed exceed the fan power, with the excess coming from the reduction in pressure of the fluid (since the flow in the narrow region will be below ambient pressure).

The reason this is possible is because the backpressure the fan has to work against is effectively set by the exit of the overall system - at that point, the pressure must equal ambient since it is exhausting to ambient. In your example, this is the pressure at the nozzle exit, and since this must equal ambient, the pressure at the back face of the fan must exceed ambient (since the pressure of the flow drops as it accelerates through the nozzle). However, if you re-expand the flow, the pressure will rise again, and if your exhaust is the same size as your fan inlet, the only backpressure acting on the fan will be whatever is required to overcome viscous effects and losses, since your diffuser will recover all of the pressure lost in the nozzle. This is why wind tunnels nearly always have a diffuser on them - it's not just to decrease exhaust jet velocity or noise, it actually dramatically reduces the power requirements for achieving a particular flow velocity since it enables the kinetic energy in the flow to exceed (possibly greatly exceed) the fan power.

 

[cjl]

Oh, and as for that wind turbine, I really don't see it as being viable. The capture area is simply too small. One benefit of non-shrouded turbines is that the blades can sweep out and interact with a truly incredible quantity of air without needing an enormous amount of material themselves. On that prototype though, it looks like the capture area is maybe 100 square meters at most, while modern wind turbines are 120+ meters in diameter (leading to a capture area in the range of 10,000 square meters). I can't see how that design could reasonably be scaled up to capture wind from a 100 by 100 meter box without it ending up more complex, heavier, and more expensive than a normal, non-shrouded horizontal axis design.

 

[eudesvera3]

Dear cjL, many, many thanks to you. You has really made my day. Your post was the one I was waiting for and, unless some participant proves the opposite, the paradox of the converging fan fed by an electric fan is after all partially true. So, according to your reasoning, it would be quite possible for a 1,500 W motor to produce an airflow kinetic power of 3,848.45 W at the throat separating the converging nozzle from the diffuser, and still have an exit airflow power less than 1,500 W, so that first law of thermodynamics is preserved. Cheers!

 

[eudesvera3]

Oh, and as for that wind turbine, I really don't see it as being viable. The capture area is simply too small. One benefit of non-shrouded turbines is that the blades can sweep out and interact with a truly incredible quantity of air without needing an enormous amount of material themselves. On that prototype though, it looks like the capture area is maybe 100 square meters at most, while modern wind turbines are 120+ meters in diameter (leading to a capture area in the range of 10,000 square meters). I can't see how that design could reasonably be scaled up to capture wind from a 100 by 100 meter box without it ending up more complex, heavier, and more expensive than a normal, non-shrouded horizontal axis design.

Good points, cjl. However I firmly believe this ground-level shrouded wind turbine can be improved a lot by a new extremely efficient renewable energy machine that will hopefully be presented to the world very soon (just a matter of not more than a couple of months). I will keep you posted.

 

[cjl]

Good points, cjl. However I firmly believe this ground-level shrouded wind turbine can be improved a lot by a new extremely efficient renewable energy machine that will hopefully be presented to the world very soon (just a matter of not more than a couple of months). I will keep you posted.

It's not a matter of efficiency. It's a matter of collection area and material quantity. At the end of the day, you can't extract more than ~59% of the kinetic energy that would pass through an area equal to your collection area in the freestream. This applies whether you use a collector design, a traditional turbine, or anything else. Current horizontal-axis wind turbines are already very close to this limit, so you aren't going to make more power without increasing the collection area or the design wind speed.

 

[Dale]

This is why wind tunnels nearly always have a diffuser on them

Is the size of the diffuser typically equal to the inlet size or is it usually even larger?

 

[eudesvera3]

It's not a matter of efficiency. It's a matter of collection area and material quantity. At the end of the day, you can't extract more than ~59% of the kinetic energy that would pass through an area equal to your collection area in the freestream. This applies whether you use a collector design, a traditional turbine, or anything else. Current horizontal-axis wind turbines are already very close to this limit, so you aren't going to make more power without increasing the collection area or the design wind speed.

IMO, you are right if the wind turbine only extracts kinetic energy from the wind and nothing else as all conventional wind turbines do. In fact, all conventional wind turbines decelerate the incoming airflow considerably. Using another approach it is possible to extract other type of energy from the wind rather than KE only.

 

[eudesvera3]

Is the size of the diffuser typically equal to the inlet size or is it usually even larger?

IMO, the size (length) of the diffuser should be at least two or three times greater than the size (length) of the converging nozzle, in order to make deceleration of airflow as gradual as possible so as to reduce as much as possible turbulence losses along the diffuser before exhausting into ambient.

 

[cjl]

Is the size of the diffuser typically equal to the inlet size or is it usually even larger?

Most of the ones I've seen have a diffuser exit area similar to the nozzle inlet area, but I'm far from an expert on wind tunnel design (I mostly do wind turbine design). Also, most of the ones I've seen have the fan at the exit of the diffuser, rather than the inlet of the nozzle, but this is primarily to reduce turbulence in the test section.

 

[cjl]

IMO, you are right if the wind turbine only extracts kinetic energy from the wind and nothing else as all conventional wind turbines do. In fact, all conventional wind turbines decelerate the incoming airflow considerably. Using another approach it is possible to extract other type of energy from the wind rather than KE only.

It's not possible to extract energy from the wind other than kinetic. You can't reduce the pressure because you don't have a low pressure reservoir to dump the exhaust into, and you can't extract thermal energy because you don't have a cold reservoir to dump the thermal energy into. Every device that extracts power from wind will decelerate the incoming airflow considerably - that's where the power is coming from.

 

[Dale]

Every device that extracts power from wind will decelerate the incoming airflow considerably - that's where the power is coming from.

I have always wondered how that works. How can the wind be decelerated? The Mach number is low so the flow should be incompressible, but with an equal inlet and outlet area I don’t see how that works.

 

[russ_watters]

I have always wondered how that works. How can the wind be decelerated? The Mach number is low so the flow should be incompressible, but with an equal inlet and outlet area I don’t see how that works.

The wind acts like it is in an expanding duct:

http://home.uni-leipzig.de/energy/ef/15.htm

 

[russ_watters]

Thank you. Can you tell me if I can close this thread and how to do it?

There isn't a way for users to close their own threads and we generally keep them open in case something else relevant comes up.

 

[eudesvera3]

It's not possible to extract energy from the wind other than kinetic. You can't reduce the pressure because you don't have a low pressure reservoir to dump the exhaust into, and you can't extract thermal energy because you don't have a cold reservoir to dump the thermal energy into. Every device that extracts power from wind will decelerate the incoming airflow considerably - that's where the power is coming from.

It's not possible to extract energy from the wind other than kinetic. You can't reduce the pressure because you don't have a low pressure reservoir to dump the exhaust into, and you can't extract thermal energy because you don't have a cold reservoir to dump the thermal energy into. Every device that extracts power from wind will decelerate the incoming airflow considerably - that's where the power is coming from.

I am sorry to disagree. It is quite possible to extract thermal energy from the wind, according to I Hirshberg (https://patents.google.com/patent/EP1841544A4) and the evidence you can see on airplane wings due to the condensation of water vapour due in turn to the drop in temperature of the airflow. On the other hand augmented or shrouded wind turbines can theoretically achieve an efficiency up to 88,88%, according to Jamieson (https://www.researchgate.net/profile/Peter_Jamieson2/publication/238184620_Beating_Betz_Energy_Extraction_Limits_in_a_Constrained_Flow_Field/links/574dbca308ae8bc5d15bf497/Beating-Betz-Energy-Extraction-Limits-in-a-Constrained-Flow-Field.pdf). However by extracting thermal unit from air or wind the efficiency could go beyond that limit,

 

[eudesvera3]

There isn't a way for users to close their own threads and we generally keep them open in case something else relevant comes up.

Thank you. It seems a reasonable policy to me.

 

[russ_watters]

I am sorry to disagree. It is quite possible to extract thermal energy from the wind, according to I Hirshberg (https://patents.google.com/patent/EP1841544A4) and the evidence you can see on airplane wings due to the condensation of water vapour due in turn to the drop in temperature of the airflow. On the other hand augmented or shrouded wind turbines can theoretically achieve an efficiency up to 88,88%, according to Jamieson (https://www.researchgate.net/profile/Peter_Jamieson2/publication/238184620_Beating_Betz_Energy_Extraction_Limits_in_a_Constrained_Flow_Field/links/574dbca308ae8bc5d15bf497/Beating-Betz-Energy-Extraction-Limits-in-a-Constrained-Flow-Field.pdf). However by extracting thermal unit from air or wind the efficiency could go beyond that limit,

Airplanes don't utilize natural wind. Natural wind is far too slow - unless in a hurricane or tornado - for compressibility to be significant.

Also; patents are not scientific sources, they are protection for inventions. The governments that issue patents care very little if the devices actually work.

...though actually this application doesn't even appear to have been accepted anyway.

 

[eudesvera3]

Airplanes don't utilize natural wind. Natural wind is far too slow - unless in a hurricane or tornado - for compressibility to be significant.

Also; patents are not scientific sources, they are protection for inventions. The governments that issue patents care very little if the devices actually work.

Thank you for your very valuable opinion, but we have to agree to disagree on this particular point. I hope forthcoming events in the field of renewable energy will prove which viewpoint is correct, yours or mine. If it is yours, I will humbly acknowledge it.

 

[Dale]

the evidence you can see on airplane wings due to the condensation of water vapour due in turn to the drop in temperature of the airflow.

The Mach numbers are substantially higher for an airplane wing. I wouldn’t use the incompressible flow assumption for an airplane, but I would for a wind turbine.

 

[russ_watters]

Thank you for your very valuable opinion, but we have to agree to disagree on this particular point. I hope forthcoming events in the field of renewable energy will prove which viewpoint is correct, yours or mine. If it is yours, I will humbly acknowledge it.

Please be aware that PF is a mainstream science site. There is only one viewpoint accepted by mainstream science:

... the equation can be used if the flow speed of the gas is sufficiently below the speed of sound, such that the variation in density of the gas (due to this effect) along each streamline can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.

https://en.wikipedia.org/wiki/Bernoulli's_principle

That's 220 mph or 100 m/s. Compressibility effects can always be said to be non-zero, but at the speed wind turbines operate at, they are a tiny fraction of a percent. This is settled science.

 

[russ_watters]

That's 220 mph or 100 m/s. Compressibility effects can always be said to be non-zero, but at the speed wind turbines operate at, they are a tiny fraction of a percent.

Let me be more specific about the numbers:

• At 10m/s, a healthy wind speed for a wind turbine, the velocity pressure from Bernoulli's equation is 61 pa or 0.06% of atmospheric; a tiny fraction of a percent.
• At 100m/s, a common speed for a jet airliner soon after takeoff, the velocity pressure is 6,100 pa or 6% of atmospheric. That's enough to start to have some significance. That's why it's the commonly cited cutoff for incompressible vs compressible flow.

 

[cjl]

I am sorry to disagree. It is quite possible to extract thermal energy from the wind, according to I Hirshberg (https://patents.google.com/patent/EP1841544A4) and the evidence you can see on airplane wings due to the condensation of water vapour due in turn to the drop in temperature of the airflow. On the other hand augmented or shrouded wind turbines can theoretically achieve an efficiency up to 88,88%, according to Jamieson (https://www.researchgate.net/profile/Peter_Jamieson2/publication/238184620_Beating_Betz_Energy_Extraction_Limits_in_a_Constrained_Flow_Field/links/574dbca308ae8bc5d15bf497/Beating-Betz-Energy-Extraction-Limits-in-a-Constrained-Flow-Field.pdf). However by extracting thermal unit from air or wind the efficiency could go beyond that limit,

That patent is incorrect. Specifically, this statement is complete nonsense:

A method of converting air internal energy into useful kinetic energy is based on air flowing through substantially convergent nozzle, which accelerates the air as the cross section of the nozzle decreases thus increasing the air kinetic energy. The increment of the kinetic energy equals to the decrement of air internal energy, i.e., air temperature

In a low-speed nozzle, the vast majority of the increased kinetic energy comes from pressure drop, not temperature drop. In addition, the exhaust of the system is exhausting to ambient, so you're constrained in what the conditions in the system can actually be. You can't use the trick I talked about above either, since you're extracting energy at the minimum area point (which prevents you from being able to recover as much in the diffuser). I would also point out that whoever wrote that patent has absolutely no idea what they're talking about with wind turbines. Case in point:

When the wind turbine propeller rotates, only fraction of the flowing air within the circle created by the propeller tips is actually flowing close enough to any of the propeller blades in order to generates aerodynamic lift on that blade. These lift forces (actually their component that lies within the propeller rotating plane and tangent to circle created by the blade segment that generates said lift component) distributed along the propeller blades create rotational moments around the propeller axis. The lift forces multiplied by their respective distance from the propeller rotating axis accumulated to a certain amount of torque, which rotate the propeller blades. Since considerable amount of air is flowing between the propeller blades, this air doesn't contribute any lift or torque to the propeller. This is one reason why such a propeller uses only about 20% of the kinetic energy of the air

Most modern wind turbines extract about 45-50%, and the theoretical limit is 59 regardless of design. Despite the large gaps between the blades, the blades are moving much faster than the wind, enabling them to meaningfully interact with basically 100% of the air that flows through the disk.

Another example:

Another inherent flaw of these wind turbines is their limit to operate on strong winds. This is because the propeller blades are heavy- about 11 tons thus the centrifugal forces at high rotation speed becomes huge and there is no economic justification to design these blades to winds more than 25 meter per second.

They do not operate in strong winds because consistent winds above 25-32 m/s (the usual range of cutout speeds for modern turbines) just don't happen often enough to make a meaningful difference in the annual energy production. Centrifugal forces do not play into it at all, since modern designs have complex control systems to regulate speed and they hit full rotor speed at something like 8 m/s.

That isn't the end of the errors in the patent either, but I suspect going through and debunking everything in it would just be a waste of both my time and the time of anyone reading this, so I'll stop there.

As for that 88% number, you're misunderstanding the paper. If the flow is constrained such that it cannot flow around the turbine but must flow through it, you can achieve that 88% number. However, a turbine with a nozzle/diffuser structure does not meet this criterion. If you try to extract too much power, there will be excessive backpressure within the structure and wind will just flow around the nozzle rather than into it. This is the same mechanism that limits conventional wind turbines, and it means that the Betz limit of 59% still applies (and it will be based on the overall collecting area, not the turbine area).