Paradox of a convergent nozzle fed by an electric fan

[Dale]

Despite the large gaps between the blades, the blades are moving much faster than the wind, enabling them to meaningfully interact with basically 100% of the air that flows through the disk.

Cool, I didn't know that! Is that true even close to the center, or is it only on the tips where the blades are moving so fast?

 

[cjl]

Right at the center, there's really not much power to be extracted, but I'd say as soon as you get perhaps 20% of the way out on the blade, you can achieve about 50% extraction of the kinetic energy of the air passing through the swept area. Usually, the tip speed ratio is about 10 or a bit less for modern designs (this is a measurement of the tip speed divided by incoming air speed, and is one of the common design parameters used), so even 20% out on the blade, the tangential speed from rotation is about twice as high as the incoming wind speed.

 

[Dale]

The wind acts like it is in an expanding duct:

So the blades must slow it down and deflect it outwards.

 

[cjl]

The outwards deflection is more of a consequence of slowing the flow down than an intentional thing done by the blades (since the density doesn't meaningfully change, and mass must be conserved), but yes, that's what happens.

 

[cjl]

Let me be more specific about the numbers:

• At 10m/s, a healthy wind speed for a wind turbine, the velocity pressure from Bernoulli's equation is 61 pa or 0.06% of atmospheric; a tiny fraction of a percent.
• At 100m/s, a common speed for a jet airliner soon after takeoff, the velocity pressure is 6,100 pa or 6% of atmospheric. That's enough to start to have some significance. That's why it's the commonly cited cutoff for incompressible vs compressible flow.

Interestingly, extremely locally, you can make a reasonable argument that air doesn't act entirely incompressibly with wind turbines. Near the tip of a modern wind turbine, the relative airspeed can be in the range of 90m/s, and the blade can be making a local Cl of around 1.5. This means there are almost definitely some significant density differences between the air on the suction and pressure sides of the airfoil out there. That having been said, this only matters locally, and in terms of the global flow, you can absolutely assume incompressibility for the sake of analysis.

 

[eudesvera3]

That patent is incorrect. Specifically, this statement is complete nonsense:

Thanks for this information. If I remember correctly in a previous post you suggested that it is possible to circumvent the problem of the back pressure on the fan caused by a convergent nozzle by just adding a divergent nozzle acting as an exhaust system and following a nozzle that in turn follows thew convergent nozzle. I wonder if by taking your suggestion and for the sake of clarifying further the matter I could pose the following problem:

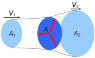
Let us assume a system formed by a convergent nozzle (Inlet), a throat, a fan, and a divergent nozzle (Exit), as shown schematically in Figures (a) and (b) below. The cross-sectional areas of the convergent nozzle, the throat, and the divergent nozzle as seen by the airflow are A1, A0 and A2, respectively. Additionally, let us suppose that A1 = A2 = 1780 cm2, and A0 = A1 / 2 = 890 cm2. The fan is driven by an electric motor whose power rating is PM = 1500 W. When the motor is operating at its maximum power rating, let us assume an airflow is exhausted to the atmosphere with a velocity Vφ2 = 20 m/s. Therefore, the power of the airflow just at the exit of the divergent nozzle is Pφ2 = 872.20 W. I would like you help me to find the answer to the following questions:

Q1. Which is the best position for placing the fan in the system, as in Fig. (a), or as in Fig. (b), in such a way as to obtain minimum pressure on the fan, and minimum fan noise?

Q2. If the exhaust velocity is Vφ2 = 20 m/s, can we infer that the airflow velocity in the throat would be Vφ0 = 40 m/s?

In a low-speed nozzle, the vast majority of the increased kinetic energy comes from pressure drop, not temperature drop. In addition, the exhaust of the system is exhausting to ambient, so you're constrained in what the conditions in the system can actually be. You can't use the trick I talked about above either, since you're extracting energy at the minimum area point (which prevents you from being able to recover as much in the diffuser). I would also point out that whoever wrote that patent has absolutely no idea what they're talking about with wind turbines. Case in point:
Most modern wind turbines extract about 45-50%, and the theoretical limit is 59 regardless of design. Despite the large gaps between the blades, the blades are moving much faster than the wind, enabling them to meaningfully interact with basically 100% of the air that flows through the disk.

Another example:
They do not operate in strong winds because consistent winds above 25-32 m/s (the usual range of cutout speeds for modern turbines) just don't happen often enough to make a meaningful difference in the annual energy production. Centrifugal forces do not play into it at all, since modern designs have complex control systems to regulate speed and they hit full rotor speed at something like 8 m/s.

That isn't the end of the errors in the patent either, but I suspect going through and debunking everything in it would just be a waste of both my time and the time of anyone reading this, so I'll stop there.

As for that 88% number, you're misunderstanding the paper. If the flow is constrained such that it cannot flow around the turbine but must flow through it, you can achieve that 88% number. However, a turbine with a nozzle/diffuser structure does not meet this criterion. If you try to extract too much power, there will be excessive backpressure within the structure and wind will just flow around the nozzle rather than into it. This is the same mechanism that limits conventional wind turbines, and it means that the Betz limit of 59% still applies (and it will be based on the overall collecting area, not the turbine area).