edd83
- 3
- 0
Homework Statement
I'm working through this question, but on the final part I've hit a brick wall so I'd be grateful for any help please.
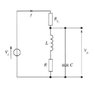
The tuned circuit has a Q-factor of 1000 and is designed to resonate at 1MHz. At resonance, the supply current I is measured at 15μA for supply voltage of 2.5V. The load resistor, RL is 10k ohms. The part of the question I'm not getting is:
Estimate the impedance offered to the supply at resonance and at the frequencies of + and - 2% from resonance
Homework Equations
I have also found that the bandwidth is 1kHz, at resonance the value of L is 25.33μH and the value of R is 0.162 ohms
The Attempt at a Solution
Could anyone suggest an equation? I'm stumped and can't think of what I need.