Partial derivative problem.... why is my answer wrong?

[Daniel Sellers]

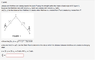
Homework Statement

The entire problem is in the attached picture. I have been checking and double checking for about an hour, found solutions online which agree with my solution, but I cannot find any answer beside -3.697 m/s which is marked wrong by the computer program.

Homework Equations

Is the homework program wrong or am I somehow missing something?

df/dt = (2x-y)/(2(x^2+y^2-xy)^(1/2))(dx/dt) + (2y-x)/(2*(x^2+y^2 -xy)^(1/2))(dy/dt)

The Attempt at a Solution

All of this works out to -3.697. I have tried rounding, leaving the answer as postive, nothing seems to work. Very frustrated.

 

[Delta2]

I also get 3.697... but where did u get the minus sign from, you input the velocities as negatives?

 

[Daniel Sellers]

I also get 3.697... but where did u get the minus sign from, you input the velocities as negatives?

The minus sign comes from the fact that the distances x and y at time t will be given by x = 21 - 5t and y = 25 - 3t hence dx/dt = -5 and dy/dt = -3. But the computer will not accept it either way. Unless anyone else can see some mistake we've both made, I will now go complain to my teacher!

Thanks

 

[PeroK]

The minus sign comes from the fact that the distances x and y at time t will be given by x = 21 - 5t and y = 25 - 3t hence dx/dt = -5 and dy/dt = -3. But the computer will not accept it either way. Unless anyone else can see some mistake we've both made, I will now go complain to my teacher!

Thanks

I agree with your answer.

 

[Ray Vickson]

The minus sign comes from the fact that the distances x and y at time t will be given by x = 21 - 5t and y = 25 - 3t hence dx/dt = -5 and dy/dt = -3. But the computer will not accept it either way. Unless anyone else can see some mistake we've both made, I will now go complain to my teacher!

Thanks

More simply: the two people get closer together as $t$ increases.

 

[DrClaude]

Have you tried fewer decimals? Four significant digits is a bit much considering the numbers given.

 

[Daniel Sellers]

It turns out that whoever wrote my homework program has never in their life heard of significant figures. Given the values involved the answer should contain only 1 sigfig, but the solution was to input SIX MORE DECIMAL PLACES from my calculator.

 

[DrClaude]

It turns out that whoever wrote my homework program has never in their life heard of significant figures. Given the values involved the answer should contain only 1 sigfig, but the solution was to input SIX MORE DECIMAL PLACES from my calculator.

And I suggested you use fewer