- #1
metastable
- 514
- 53
I have a question about this picture:
It shows matter traveling at relativistic velocities away from a black hole:
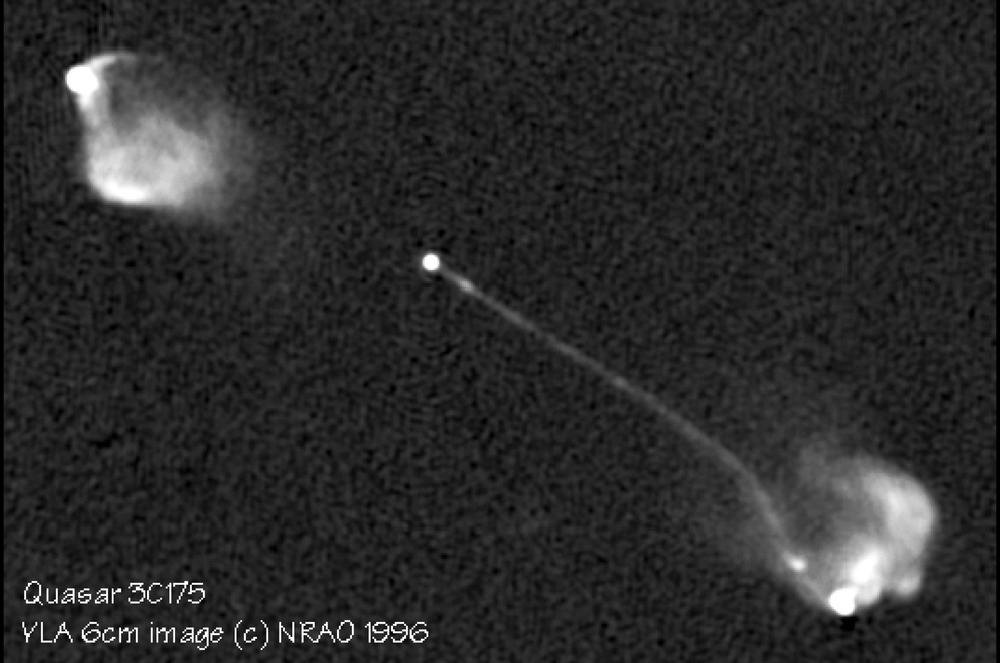
"Figure 5.21: This VLA image of the radio-loud quasar 3C 175 shows the core, an apparently one-sided jet, and two radio lobes with hot spots of comparable flux densities. The jet is intrinsically two sided but relativistic, so Doppler boosting brightens the approaching jet and dims the receding jet. Both lobes and their hot spots are comparably bright and thus are not moving relativistically. Image credit: NRAO/AUI/NSF Investigators: Alan Bridle, David Hough, Colin Lonsdale, Jack Burns, & Robert Laing."
I'm confused by the image, because in a different thread it was stated:
If the deceleration due to gravity is independent of the outward speed, how is it thought that the particles that have relativistic velocity with respect to the black hole retain a velocity which is so close to the speed of light after traveling many so many light years "upwards" away from the super massive black hole?
It shows matter traveling at relativistic velocities away from a black hole:
"Figure 5.21: This VLA image of the radio-loud quasar 3C 175 shows the core, an apparently one-sided jet, and two radio lobes with hot spots of comparable flux densities. The jet is intrinsically two sided but relativistic, so Doppler boosting brightens the approaching jet and dims the receding jet. Both lobes and their hot spots are comparably bright and thus are not moving relativistically. Image credit: NRAO/AUI/NSF Investigators: Alan Bridle, David Hough, Colin Lonsdale, Jack Burns, & Robert Laing."
I'm confused by the image, because in a different thread it was stated:
the deceleration due to gravity is independent of the outward speed.
If the deceleration due to gravity is independent of the outward speed, how is it thought that the particles that have relativistic velocity with respect to the black hole retain a velocity which is so close to the speed of light after traveling many so many light years "upwards" away from the super massive black hole?