Particle traveling towards a plate with an Electric Field

[doggydan42]

Homework Statement

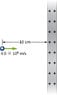
From a distance of 10 cm, a proton is projected with a speed of $v = 4.0 × 106 \frac{m}{s}$ directly at a large, positively charged plate whose charge density is $\sigma = 2.0 × 10^{-5} \frac{C}{m^2}$. (See below.) (a) Does the proton reach the plate? (b) If not, how far from the plate does it
turn around?

Homework Equations

$$\vec E = \frac{1}{4\pi \varepsilon_0} \int_{Surface} \frac{\sigma}{r^2} \,dA \hat r$$

The Attempt at a Solution

I understand that once you find the electric field, you can multiply by the charge to find the force, than set that equal to $m\vec a$ and solve for a knowing the mass of the proton. Then use kinematics to find how far it will travel.

Though to find the electric field, I am unsure of how to set $dA$, $\hat r$, and $r$. I am also unsure of what to integrate over.

Thank you in advance.

 

[Orodruin]

I strongly suggest using the potential instead of the field.

You need to integrate over the surface charge - or you can use symmetry arguments.