TSny
Science Advisor
Homework Helper
Gold Member
- 14,803
- 4,801
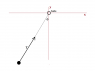
No. There is no way for those forces, as drawn, to add up to zero.Vibhor said:Do you think the attached picture correctly represents the forces acting on the particle in second quadrant ?

 .You are right. Can I say path traversed would be circular .
.You are right. Can I say path traversed would be circular .