- #1
GabeRM
- 12
- 7
- TL;DR Summary
- Rusty w/ hand calcs. Need help with figuring out the impact force generated by a pendulum hammer.
Hi all,
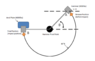
I'm a bit embarrassed but I'm extremely rusty with a lot of engineering principles. I've mainly been working in automation and controls within a manufacturing setting and have not done anything like this in ages. Anyways, I have a problem I need to solve and I need to determine the impact force in Gs exerted on the Anvil table by the hammer in the attached image. Some guidance in how to solve this problem/sources of where I can find additional material to refresh on this is greatly appreciated.
Thanks!
I'm a bit embarrassed but I'm extremely rusty with a lot of engineering principles. I've mainly been working in automation and controls within a manufacturing setting and have not done anything like this in ages. Anyways, I have a problem I need to solve and I need to determine the impact force in Gs exerted on the Anvil table by the hammer in the attached image. Some guidance in how to solve this problem/sources of where I can find additional material to refresh on this is greatly appreciated.
Thanks!