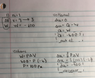MauricioValdez
- 1
- 0
Homework Statement
[/B]
Okay guys I have attached a picture of my work.
I guess my question really is, if they are telling me that Cp =7/2 am I allowed to assume that I am dealing with a diatomic gas? If so, that would change my equation to (5/2) instead of (3/2) correct? and therefore my answer would be right.
Homework Equations
[/B]
dU=(3/2)nRdT
The Attempt at a Solution
i have attached my work. My first part is right and second is wrong
Attachments
Last edited by a moderator: