Physics Graph Word Problem -- Motion of a person skiing down a slope

[Lui4]

Homework Statement

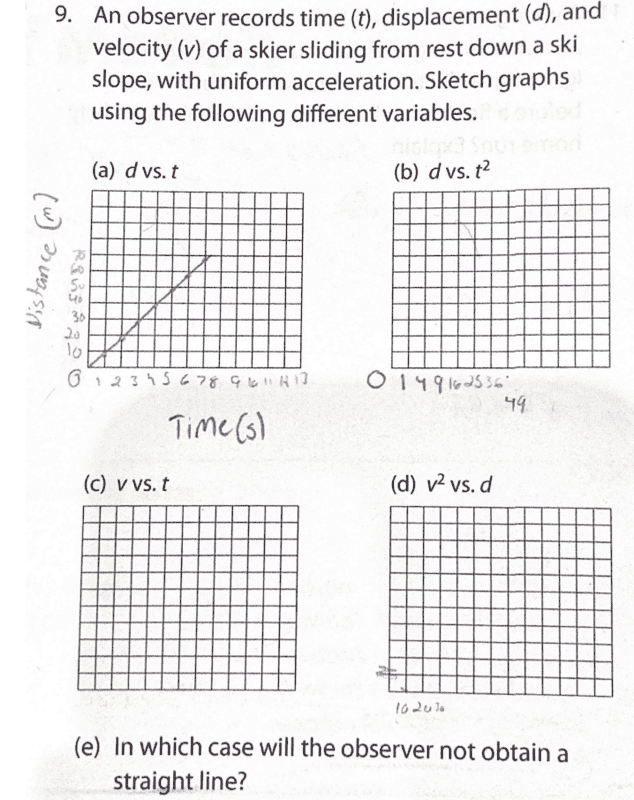
An observer records time (t), displacement (d), and velocity (v) of a skier sliding from rest down a ski slope, with uniform acceleration. Sketch graphs using the following different variables.

Relevant Equations

The graphs. See below.

I was able to do the first graph knowing that acceleration is 9.8 and my distance goes up by 10s (y-axis) and my time goes up by 1s (x-axis). For the other 3 graphs, I'm not sure where to begin because I don't know how to figure out my velocity

 

[hmmm27]

What does the phrase "uniform acceleration" mean, with regards to time, displacement and velocity ? Are you familiar with the 'SUVAT' equations ?

 

[Delta2]

You first must write the relevant equations and then do the graphs!
So , let's start from scratch, what equation do you know, in the case of moving in a straight line with uniform acceleration a, that relates d (displacement) and t(time), and given that the initial velocity $v_0=0$,i.e the skier starts from rest.

 

[Lui4]

What does the phrase "uniform acceleration" mean, with regards to time, displacement and velocity ? Are you familiar with the 'SUVAT' equations ?

I'm not sure what it means either but the guess I made is 9.8 because the gravitational pull of the Earth is 9.8m/s. The only information given is what is shown in the pictures I attached of the question.

 

[Lui4]

You first must write the relevant equations and then do the graphs!
So , let's start from scratch, what equation do you know, in the case of moving in a straight line with uniform acceleration a, that relates d (displacement) and t(time), and given that the initial velocity $v_0=0$,i.e the skier starts from rest.

I'm not sure of what equation to use in a straight line with uniform acceleration. The guess that I made is that we go up by 9.8m/s because 9.8 is the gravitational pull of the earth. I'm not sure where to start with the problem at all.

 

[Delta2]

I'm not sure of what equation to use in a straight line with uniform acceleration.

That is basic theory, and if you don't know this I doubt if I ll be able to help you. Oh well, let's see does the equation $$d=\frac{1}{2}at^2$$ ring a bell to you?

 

[Lui4]

Yes this does ring a bell this is taken from the formula d=vot+1/2at^2. Now that I know this formula what exactly do I need to do with it as there is no numbers given. The solution that I think using this equation would be 0.5 x 9.8 which would leave us at D=4.9t^2. I don't think that is correct but that is my thought process.

 

[hmmm27]

Why do you think that you are required to mark numbers on the graphs ?

 

[Delta2]

Yes this does ring a bell this is taken from the formula d=vot+1/2at^2. Now that I know this formula what exactly do I need to do with it as there is no numbers given. The solution that I think using this equation would be 0.5 x 9.8 which would leave us at D=4.9t^2. I don't think that is correct but that is my thought process.

ok much better, though your final equation D=4.9t^2 is not necessarily correct, because we don't know if the acceleration of the skier is equal to 9.8, all we are given from the problem data is that his acceleration is uniform (constant). The acceleration of the skier would be 9.8 if the skier was doing a free fall, however he doesn't do a free fall, he moves down a slope (incline).

So we ll just keep the unknown acceleration $a$ of the skier as parameter to the equation $$d=\frac{1}{2}at^2$$. Using this equation you can make the first two graphs a) and b). So let's start with a) what do you think the graph for a) will be given that equation that relates d and t?

 

[Lui4]

Okay I understand the point you made of if the skier was in free fall it would be 9.8 but since he is moving down a slope It's not 9.8. I also understand that the skier moves at a constant rate. The last part of your response is where I'm confused. My only guess would be 1/2 is equal to 0.5 meaning it would be something like d=0.5at^2 but that's the same thing just in decimal form. My original question is how to figure out the information I need to plot. You have given me the formula but I don't know what to do with it.

 

[Lui4]

Why do you think that you are required to mark numbers on the graphs ?

Mark Numbers? We need numbers for the x and y-axis and that's what I'm trying to figure out. After we figure that out I don't know what to plot.

 

[Delta2]

Okay I understand the point you made of if the skier was in free fall it would be 9.8 but since he is moving down a slope It's not 9.8. I also understand that the skier moves at a constant rate. The last part of your response is where I'm confused. My only guess would be 1/2 is equal to 0.5 meaning it would be something like d=0.5at^2 but that's the same thing just in decimal form. My original question is how to figure out the information I need to plot. You have given me the formula but I don't know what to do with it.

yes 1/2 is the same as 0.5.

To plot the graph a) label the horizontal axis with the values of time 0,1,2,3,4,..., and the vertical axis as 0,$a$,$2a$,$3a$,...,. You know for example for t=1 we have $d=0.5a(1^2)=0.5a$, for t=2 we ll have $d=0.5a(2^2)=2a$, and so on you can plot the graph. If you plot it well, it will be a parabola with its vertex at the point (0,0).

To plot the graph b) you need to do a small trick: Set $x=t^2$ and then you will have $d=0.5ax$ and plot this graph with the horizontal axis the values of x=0,1,2,3,... and the vertical axis as in graph a). if you plot it will it will be a sloped line passing through the origin.

 

[hmmm27]

I also understand that the skier moves at a constant rate.

A constant rate of what ? Velocity ?

Look, if it helps get you in the swing of things, use a=1 or 2.

So,
at t=0, what is the displacement ?
at t=1, what is the displacement ?
at t =... you can see where I'm going with this, yes ?

 

[Delta2]

Look, if it helps get you in the swing of things, use a=1 or 2.

Yes that might be a good advice if he has difficulty considering distance d with the unknown acceleration $a$ as parameter.

 

[hmmm27]

I'd prefer if he started juggling the equations first, as you indicated a few posts ago. OTOH grinding through has its advantages.