AgustRunarsson
- 1
- 0
Note: I'm sorry if I have to use the template, but I already have the solution, I just do not understand it and need help understanding it.
1. Question: A firework explodes at a 40 metre height and gives off a bang which measures at 100 dB at ground level. What is the power of the sound that comes off the firework?
This is the solution:
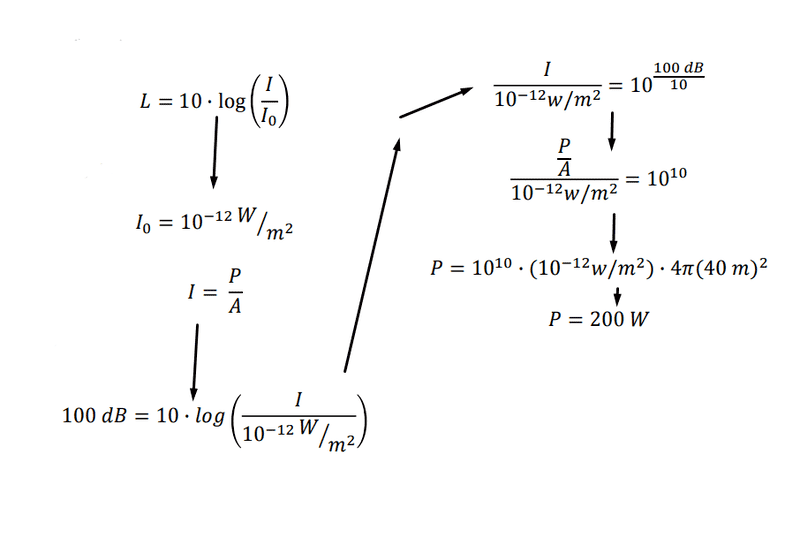
I understand what is going on, for the most part.
What I do not understand exactly is at the second part the "100 dB" becomes 10^100dB/10 which removes the log. How? I understand that the exponent is 10 in "10*log" but I don't really understand how the 10 comes from in the exponent of the 10 itself.
Any help would be appreciated. Thanks!
1. Question: A firework explodes at a 40 metre height and gives off a bang which measures at 100 dB at ground level. What is the power of the sound that comes off the firework?
This is the solution:
I understand what is going on, for the most part.
What I do not understand exactly is at the second part the "100 dB" becomes 10^100dB/10 which removes the log. How? I understand that the exponent is 10 in "10*log" but I don't really understand how the 10 comes from in the exponent of the 10 itself.
Any help would be appreciated. Thanks!
