Physics work problem - mastering physics

AI Thread Summary
The discussion revolves around calculating the work done by a 15-Newton force using the equation W = F·s·cos(θ). The initial calculation yielded W = 15*cos(140°)*160 = -1838.506, but the user received feedback from Mastering Physics indicating potential errors in rounding or significant figures. A key point raised is the requirement for angle measures to be in radians, which may impact the calculation. Despite this, the user argues that the cosine value should not affect the overall answer. The conversation highlights the importance of precision in calculations and the nuances of using different angle measurement systems in physics problems.
Shayna
Messages
13
Reaction score
0
Physics work problem -- mastering physics

Homework Statement


163337B.jpg
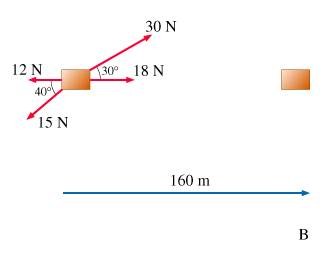Find the work W done by the 15-Newton force.

Homework Equations


W=\vec F\cdot\vec s=\left|\vec F\right|\left|\vec s\right|\cos \theta

The Attempt at a Solution


W= 15*cos140*160 = -1838.506
I don't know why mastering physics was telling me "Not quite. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures."
 
Physics news on Phys.org


I don't know if you already figured this out, but the only thing I can think of (and it's not really even related to the error you were getting) is that Mastering Physics requires angle measures to be in radians.
 


yes but that shouldn't be affecting the answer though, cos140degree = cos(14/9)pai
Thanks though
 

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Understanding work in translation and rotation of a magnetic dipole
Replies
1
Views
2K
Is the line integral of tangential force in pendulum equal to the negative of change in potential energy?
Replies
3
Views
884
What is the induced magnetic force on this closed current loop?
Replies
12
Views
2K
Is potential energy defined only for internal conservative forces?
Replies
15
Views
1K
Simple Ramp motion problem, but going full vector mode
Replies
29
Views
2K
Circular motion of a mass on a string on an inclined plane
Replies
14
Views
4K
Work done pushing a spring from the side
Replies
9
Views
2K
Work Done by Elevator Cable in Sample Problem 7-6
Replies
2
Views
3K
Understanding Work-Energy Theorem: Solving an Exercise with Different Solutions
Replies
11
Views
3K
Effect of different magnetic fields on a magnetic dipole
Replies
25
Views
1K

Hot Threads

Recent Insights

Back
Top