Mdhiggenz
- 324
- 1
Homework Statement
can you judge the diagram I want to make sure i have the forces being exerted in the correct order.
That's the correct direction. If you add the vectors correctly, you will also get the correct magnitude !Mdhiggenz said:Homework Statement
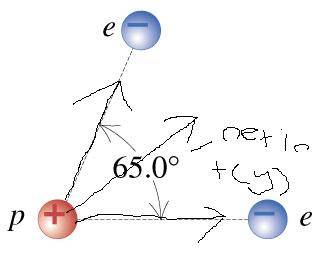
can you judge the diagram I want to make sure i have the forces being exerted in the correct order.
Homework Equations
The Attempt at a Solution
No. That won't give the correct answer.Mdhiggenz said:One more question sam. I have want to make sure I clearly understand, Let's call the top top electron E1, and bottom E2.
I only have to get the Cosine of the bottom election because it is on the horizontal and not on an angle, but for E1 I have to get both the sin and cos.
And to get the magnitude I can simply add squareroot fsin(theta)+2fcos(theta) ?
Earlier you said "squareroot fsin(theta)+2fcos(theta)".Mdhiggenz said:Pretty much my theta is 65 degrees and what I am doing is this
√(F)^2+(Fsin(65))^2+(Fcos(65))^2
and I don't understand how it isn't giving me the answer
Now that a complete answer to a similar, but more detailed problem has been given in another of your threads, I'll give the solution here, arrived at in two ways.Mdhiggenz said:Pretty much my theta is 65 degrees and what I am doing is this
√(F)^2+(Fsin(65))^2+(Fcos(65))^2
and I don't understand how it isn't giving me the answer