TopologyisGeometry
- 2
- 2
- Homework Statement
- Plot the wave function ##u(r)## as a function of ##r## from 0 to 10 fm. Since ##u##is not normalized, you won't need units on the y axis.
- Relevant Equations
- $$\frac{-\hbar^2}{2\mu}\frac{d^2u(r)}{dr^2}+V(r)u(r) = Eu(r)$$ Where $$V(r) = \begin{cases}-V_0 \quad r<R\\ 0\quad r>R\end{cases}$$ Which has the solutions previously found to be
$$u(r)=\begin{cases}A\sin(kr)\quad r<R\\ De^{-\kappa r}\qquad r>R\end{cases}$$
To plot ##u(r)## we need to find the solutions for each region. Which is in the relevant equations part. Now, I have to do this numerically. Using python 3.7 I made an ##u## which is filled with zeros and a for loop with if/elseif statement, basically telling it to plot values for whenever ##r<R## and ##r>R##. Here is the plot generated by my simple code
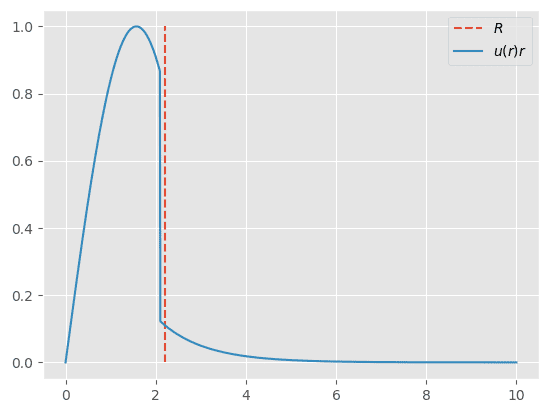
Due to continuity at $r=R$ they need to have the same value. Which makes me believe that this is a root finding problem, basically ##A\sin(kr)-De^{-\kappa r}=0## Now I don't know how to implement this onto my code, at first I thought make another elif statement for when ##r==R## to use the roots as the values, how would I go on about this problem? Have I forgotten something?
Due to continuity at $r=R$ they need to have the same value. Which makes me believe that this is a root finding problem, basically ##A\sin(kr)-De^{-\kappa r}=0## Now I don't know how to implement this onto my code, at first I thought make another elif statement for when ##r==R## to use the roots as the values, how would I go on about this problem? Have I forgotten something?