- #1
squareroot
- 76
- 0
1. Homework Statement
I've been using a recurrence relation from "Adv. in Physics"1966 Nr.57 Vol 15 . The relation is :
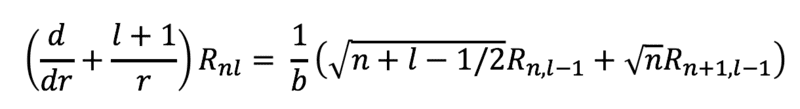
where Rnl are radial harmonic oscillator wave functions of form:
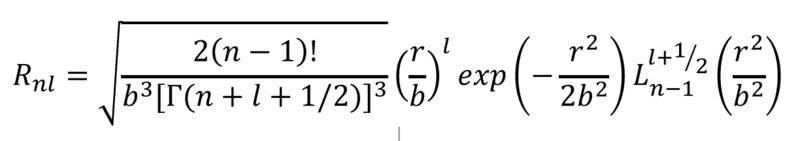
The problem is that I can't prove the relation above with the form of Rnl given by the author(above). I've been trying to check this using Mathematica. The form in which I need to use this is the following:
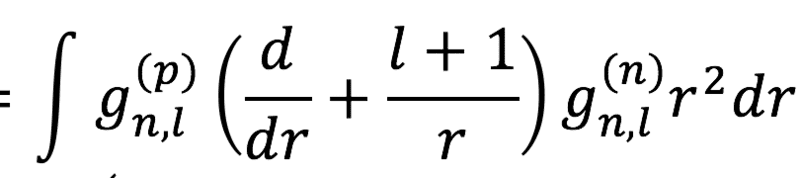
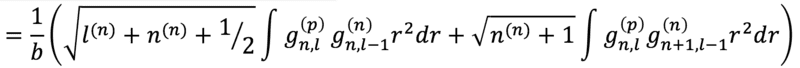
Here, I use the Rnl's as radial wave-functions for neutrons and protons and multiply the first relation with Rprotonnl and integrate over spherical coordinates.(P.S the R's where noted by g's ).
My questions is why would a relation like this only hold if the R's(or g, respectively) are normalized? Should't this relation hold for any radial wavefunctions? Where does the normalization condition comes from?
The above relations are equivalent with let's say
$$ | \alpha \rangle = a |\beta \rangle + b|\gamma \rangle $$
and by multiplying with the bra ## | \alpha \rangle ## to the left one gets
$$ \langle \alpha | \alpha \rangle = a \langle \alpha | \beta \rangle + b \langle \alpha | \gamma \rangle $$
This is kind of my case above, but from my reasoning it should hold with no dependence on the normalization of the functions.
Thank you!
I've been using a recurrence relation from "Adv. in Physics"1966 Nr.57 Vol 15 . The relation is :
where Rnl are radial harmonic oscillator wave functions of form:
The problem is that I can't prove the relation above with the form of Rnl given by the author(above). I've been trying to check this using Mathematica. The form in which I need to use this is the following:
Here, I use the Rnl's as radial wave-functions for neutrons and protons and multiply the first relation with Rprotonnl and integrate over spherical coordinates.(P.S the R's where noted by g's ).
My questions is why would a relation like this only hold if the R's(or g, respectively) are normalized? Should't this relation hold for any radial wavefunctions? Where does the normalization condition comes from?
The above relations are equivalent with let's say
$$ | \alpha \rangle = a |\beta \rangle + b|\gamma \rangle $$
and by multiplying with the bra ## | \alpha \rangle ## to the left one gets
$$ \langle \alpha | \alpha \rangle = a \langle \alpha | \beta \rangle + b \langle \alpha | \gamma \rangle $$
This is kind of my case above, but from my reasoning it should hold with no dependence on the normalization of the functions.
Thank you!
Homework Equations
The Attempt at a Solution
Attachments
Last edited: