Plotting the waveforms of the harmonic components

[kibara]

Homework Statement

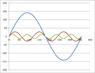
Hello everyone, I am currently experiencing a problem plotting harmonics in Excel.
I'm only able to plot the fundamental wave properly, I can't figure out how to plot the 3rd and 5th harmonic as they have a different frequency. Can you point me in the right direction, please...

Homework Equations

vf=141.44sin(240*PI*t) - fundamental
v3=28.29sin(720*PI*t) - 3rd harmonic
v5=14.14sin(1200*PI*t - 1.2*180/PI) - 5th harmonic

The Attempt at a Solution

Excel equation for vf
Degrees 0 to 360 (interval of 15) Column A2 to A26
=SIN(A2*PI()/180)*141.44
By using the above values I'm able to obtain a scatter plot but for the 3/T and 5/T the above does not work
I know that T=0.0083s not sure what else to add at the moment.

 

[BvU]

Hello kibara,

If in column A you plot from 0 to 360, then your independent variable is not time, but the phase (in, o horror, degrees ).

So in column C you want
=SIN(3*A2*PI()/180)*28.29 and not
=SIN(3 /0.0083 *A2*PI()/180)*28.29

 

[jambaugh]

Your fundamental has an angular frequency of
$$\omega_f = 240\pi$$
divided by whatever is your time unit. You are rescaling to degree angle measure. The relation, in radians is:
$$\theta = \omega_f \cdot t$$
but you are then converting to degrees. Note that $1^\circ = \frac{2\pi}{180}$ which means you can treat the degree symbol itself as this number.
So your A2 through A26 entries are values of:
$$\theta^\circ = \frac{2\pi \omega_f}{180}\cdot t$$
You are then converting these back into radians within your trigonometric function: SIN(A2*PI()/180)*141.44 = $141.44 \sin(\omega_f t)$
You want to then change the frequency (and amplitude) for your harmonics and so you want to first divide out the old frequency and then multiply by the new one:
$$\sin(\omega_n t) = \sin(\frac{\omega_n}{\omega_f}\cdot \omega_f t)$$
which means you need to add a factor of the ration of the angular frequencies to your trig function:
Note that $\omega_3 = 720\pi$ and so $\omega_3/\omega_f = 720/240 = 3$. That's why it's the 3rd harmonic. So add a factor of 3 in your trig function:

SIN(3*A2*PI()/180)*28.29 would be the entry for angle in A2.

I am sorry to take the long way around to this simple answer but the steps are those you should, yourself, take when translating your problem to the excel spread sheet.
Doing so should make the answer to your question relatively clear to you from the start.

 

[kibara]

Good morning Everyone (if European time)

Thanking you kindly for your help. I can see the solution is relatively easy. I now plotted my graph using Excel. BvU seems that you missed v5 phase shift.

for v3 I used =SIN(3*A3*PI()/180)*28.29 , =SIN(A3*PI()/60)*28.29 works fine too.

for v5 I used =Sin(w5t-1.2*180/PI)*14.14

https://ibb.co/gvKUyJ

Have a great Sunday ! :)

 

[BvU]

BvU seems that you missed v5 phase shift.

Well observed ! Demonstrates to me that you master this exercise !