Potential and Electric Fields: Understanding Charges and Fields on a Line

[fogvajarash]

Homework Statement

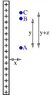
Consider a line of length L=0.950 m and uniform positive charge per unit length λ=2.9 μC. Point A is a distance x=0.23 m from the center of the line, while B is the same distance from the line but a distance y=0.28 m farther along the line; point C is a distance z=0.050 m farther along the line than B.

Answer true or false for the following statements.
a) The potential at A is higher than the potential at B.
b) The potential at B is higher than the potential at C.
c) The electric field has a horizontal component at A.
d) The electric field has a horizontal component at B.
e) The electric field has a vertical component at A.
f) The electric field has a vertical component at B.
g) If the line were made of a conductor, the charges would re-arrange themselves rather than remaining in this configuration.

Homework Equations

-

The Attempt at a Solution

I'm trying to understand how to relate potential and electric field in this situation. As we have a line, we would have that the electric field is not pointing outwards of the line, as we would only have an horizontal component in A. On the other hand, on points B, C we would have an electric field both with a horizontal and vertical component. However, I'm having trouble with the potential questions, I'm guessing that they should be equal as we do not really care about components in this case. On the other hand, I am not sure what g. is asking for.

Thank you in advance.

 

[Adithyan]

First, let us talk about option 'g' since it is easy. Have a look a Gauss Law : http://en.wikipedia.org/wiki/Gauss's_law
(Hint: Field inside a conductor must be zero). Now relate charge distribution of the rod with Gauss Law to make the field inside zero.

Then, coming to potentials, I guess you have a problem regarding the first two options. The basic definition of change in electric potential is -∫E.dr(mind the negative sign). Coloumbic force is a conservative one. So it doesn't matter how you reach point b. Now, try reaching the point B by first reaching point 'A' and then climbing upwards. Also take care of the point that, while climbing upwards, bother only about the vertical components (Think why?).

Think about it; do inform me if you have any problem.

Regards
ADI.