Preserving Magnetic Polarity in a Revolving Reference Frame

[kmarinas86]

***not homework for any class***

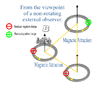
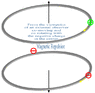
Title: "Preserving Magnetic Polarity in a Revolving Reference Frame"
Problem: How can a revolving reference frame (assuming an uncharged observer with negligible mass) observe the same polarity for a magnet in the case where the rotational speed is great enough to observe the source current revolving in the opposite direction, or not at all?

Note: The first image says "From the viewpoint of a non-rotating external observer." With that I mean "no rotation with respect to another observer".

 

[bcrowell]

Note: The first image says "From the viewpoint of a non-rotating external observer." With that I mean "no rotation with respect to another observer".

There is nothing wrong with the original label on the figure. Rotational motion is not relative in relativity, it's absolute. For example, an observer in a rotating frame detects a Sagnac effect.

Problem: How can a revolving reference frame (assuming an uncharged observer with negligible mass) observe the same polarity for a magnet in the case where the rotational speed is great enough to observe the source current revolving in the opposite direction, or not at all?

The rotating and nonrotating observers have to agree on whether the two rings collide, but they do not have to agree on the magnetic force between them. What one observer sees as a net attraction due to some combination of electric and magnetic forces, the other observer will see as a net attraction due to some other combination.

You don't state whether the rings are meant to be electrically neutral over all, or whether the charges marked in green and red are the only ones present.

Let's assume that the rings are electrically neutral. In the nonrotating frame, there is only a magnetic force. In the rotating frame, there are both electric and magnetic forces. The sum of these must be attractive, so there must be an attractive electric force that is stronger than the magnetic one. This net attractive electric force is the sum of four different forces between four different combinations of charges (+ on top with + on bottom, + on top with - on bottom, etc.), each of which is nonzero because each charge density experiences a different Lorentz contraction (and these Lorentz contractions are also different at different points on the rings).

If the rings are not electrically neutral, I think the above analysis holds with obvious modifications.

 

[kmarinas86]

There is nothing wrong with the original label on the figure. Rotational motion is not relative in relativity, it's absolute. For example, an observer in a rotating frame detects a Sagnac effect.The rotating and nonrotating observers have to agree on whether the two rings collide, but they do not have to agree on the magnetic force between them. What one observer sees as a net attraction due to some combination of electric and magnetic forces, the other observer will see as a net attraction due to some other combination.

You don't state whether the rings are meant to be electrically neutral over all, or whether the charges marked in green and red are the only ones present.

The keyword is "residual". The residual charge could represent 1% of the total charge. It is the net charge of each ring itself.

So you have electrical repulsion between like net charges and electrical attraction between opposite net charges.

First image: In one reference frame, the magnetic poles are aligned in the same direction.

Second image: In another reference frame, are the magnetic poles necessarily aligned in the same direction? Does the pole on the bottom really reverse? If not, how does relativity prevent it from reversing in that frame of reference? Also, do all the poles that exist in the first reference frame exist in the second one?

Note: In the second image, the observer has the same angular velocity as the net negative charge in the center, as well as having the same orbital axis. In other words, their paths make for two concentric circles, which makes that central net negative charge stationary relative to that observer.

 

[Dale]

Are there three rings of current, or just two. I don't understand the relationship of the two diagrams.

I think it is an interesting question, but you may not realize that the magnetic field is frame-variant. So there is in general no guarantee that it will have the same polarity in all frames. In fact, in non-inertial frames there may only be the electromagnetic tensor and the coordinates may be messy enough that you can't even point to one component and say "that is a component of the magnetic field".

 

[kmarinas86]

Are there three rings of current, or just two. I don't understand the relationship of the two diagrams.

Isn't it true that whether there is current observed in the given reference frame, or not, is contingent on whether the net charge is in motion relative to the given frame of reference?

I think it is an interesting question, but you may not realize that the magnetic field is frame-variant. So there is in general no guarantee that it will have the same polarity in all frames.

Wouldn't that imply that the system in question has different futures per each reference frame? For example, some futures would be based on all three dipoles aligning with each other, while others would be based on one dipole in opposition to the other two, and others yet would involve only two dipoles? Why would different futures follow from something so basic, like the relative motion of charges? Or are different futures somehow avoided?

 

[bcrowell]

The keyword is "residual". The residual charge could represent 1% of the total charge. It is the net charge of each ring itself.

It's not correct to describe the rings by saying that the net charge is moving in a certain direction at a certain speed. The net charge is a number, not an object. If the net charge is the sum of various charges in different states of motion, then those charges Lorentz-transform in different ways.

Second image: In another reference frame, are the magnetic poles necessarily aligned in the same direction?

No. That's essentially what you've proved.

Isn't it true that whether there is current observed in the given reference frame, or not, is contingent on whether the net charge is in motion relative to the given frame of reference?

No, because the net charge is a number, not an object. However, it is true that it is frame-dependent whether the current is zero or nonzero.

Wouldn't that imply that the system in question has different futures per each reference frame? For example, some futures would be based on all three poles aligning with each other, while others would be based on one pole in opposition to the other two.

There are both magnetic torques and electric torques in the rotating frame. The alignment of the rings (but not their magnetic dipole moments) is frame-invariant, but the description of the alignment process in terms of electrical or magnetic torques is not.

 

[Dale]

Isn't it true that whether there is current observed in the given reference frame, or not, is contingent on whether the net charge is in motion relative to the given frame of reference?

Huh? I don't understand this response to my question. Are there three rings or two? Please explain the relationship between the two diagrams.

Wouldn't that imply that the system in question has different futures per each reference frame? For example, some futures would be based on all three dipoles aligning with each other, while others would be based on one dipole in opposition to the other two, and others yet would involve only two dipoles? Why would different futures follow from something so basic, like the relative motion of charges? Or are different futures somehow avoided?

No, the different reference frames don't have different futures. However, Maxwell's equations in terms of electric and magnetic fields will not look the same when expressed in a non-inertial coordinate system.

 

[kmarinas86]

Huh? I don't understand this response to my question. Are there three rings or two? Please explain the relationship between the two diagrams.

There are three rings.

The center ring is not visible in the second diagram.

First picture:

Top ring: Positive residual charged ring rotates to generate a north pole pointing to the top of the picture.

Center ring: Negative residual charged ring rotates to generate a north pole pointing to the top of the picture.

Bottom ring: Negative residual charged ring rotates to generate a north pole pointing to the top of the picture.

As you can see, the negative residual charged rings rotate opposite of the positive residual charged ring to generate magnetic fields of the same polarity.

Let's say for example sakes, the Top and Bottom rings have a orbital frequency of 1 Hz, while the Central ring has an orbital frequency of 1MHz, and that the distance between them is large enough for them to not fly out of the sides page within an appreciable time span of, say, one hour.

Second picture:

Top ring: Positive residual charge is seen orbiting the same direction as before, with the north pointing to the top of the picture. But now, you have a 1Hz component and a 1MHz component overlapping each other. However, since the movement about the axis of the observer's orbit is much faster in terms of both r and omega, and thus v, most of this magnetic field is attributed to the 1MHz component.

(Not shown) center ring: No magnetic field here is generated whatsoever because it is stationary relative to the observer. So I just show the negative residual charge.

Bottom ring: Negative residual charge is seen rotating the opposite direction as before, so its north pole points to the bottom of the picture. But now, you have a 1Hz component and a 1MHz component overlapping each other. However, since the movement about the axis of the observer's orbit is much faster in terms of both r and omega, and thus v, most of this magnetic field is attributed to the 1MHz component.

No, the different reference frames don't have different futures. However, Maxwell's equations in terms of electric and magnetic fields will not look the same when expressed in a non-inertial coordinate system.

If the magnetic field polarity reverses for one of the dipoles, you would expect the difference to be accounted for as a dipole in the electromagnetic field. But since the magnetic portion was changed by more than the original magnitude, due the change in sign, this would imply that the electric component of the magnetic field must somehow make up for it. No matter what, the electromagnetic field must somehow preserve the quality of a 1/r^2 coulomb force overlapping a 1/r^3 magnetic dipole force, even if somehow that means the generation of a 1/r^3 electric dipole.

In the second image:

Is a 1/r^3 electric dipole force created for the center charge according to the observer who is stationary with respect to it? I consider this to be the most important question.

And then what if I have two more rings just like the top and bottom, but swapped, so that I have one positive ring and one negative ring at the top right, and one positive ring and one negative ring on the bottom right. How then does the reference frame generate multiple 1/r^3 electric dipoles amongst all of them to preserve the function 1/r^3 function of the magnetic dipoles? Wouldn't that mean that all north would have to replaced by one type of charged pole of each dipole, say, -, while all south would have to be replaced by the opposite charged pole of each dipole, say, +?

 

[Dale]

(Not shown) center ring: No magnetic field here is generated whatsoever because it is stationary relative to the observer. So I just show the negative residual charge.

Thanks, that's the part I was missing.

No matter what, the electromagnetic field must somehow preserve the quality of a 1/r^2 coulomb force overlapping a 1/r^3 magnetic dipole force, even if somehow that means the generation of a 1/r^3 electric dipole.

Yes, but don't forget that beyond changing fields there will also be changes to Maxwell's equations and the Lorentz force law. So your usual understanding of what kinds of fields produce what kinds of forces may be completely wrong in a non-inertial frame.

 

[kmarinas86]

Thanks, that's the part I was missing.

Yes, but don't forget that beyond changing fields there will also be changes to Maxwell's equations [what changes?] and the Lorentz force law [what changes?]. So your usual understanding of what kinds of fields produce what kinds of forces may be completely wrong in a non-inertial frame.

I still have three more questions:

In the second image:

• Is a 1/r^3 electric dipole force created for the center charge according to the observer who is stationary with respect to it? I consider this to be the most important question.
  
• How does the reference frame generate multiple 1/r^3 electric dipoles to counteract the relative difference of the magnetic dipoles of the top and bottom loops (when comparing pictures one and two)?
  
• Wouldn't that mean that all north would have to replaced by one type of charged pole of each dipole, say, -, while all south would have to be replaced by the opposite charged pole of each dipole, say, +?

 

[Dale]

What you need to do to answer those three questions is to set up the sources, the fields, and the forces, in the non-rotating frame using the covariant formulation of classical electromagnetism. Then you need to transform into the rotating frame. That will give you the sources, the forces, and the fields in the rotating frame.

http://en.wikipedia.org/wiki/Covariant_formulation_of_classical_electromagnetism

 

[kmarinas86]

What you need to do to answer those three questions is to set up the sources, the fields, and the forces, in the non-rotating frame using the covariant formulation of classical electromagnetism. Then you need to transform into the rotating frame. That will give you the sources, the forces, and the fields in the rotating frame.

http://en.wikipedia.org/wiki/Covariant_formulation_of_classical_electromagnetism

But what if:
* I am the observer in the second picture.
* I do not know what the non-rotating frame is.
* I do not know to which I am rotating.
* And I see the following in second picture, except I do not know that the charge in the center which appears to be stationary is actually orbiting around the same axis I am.

Do I assume then that the charge in the center has no polar electromagnetic field when I don't know that is actually orbiting an axis that it shares with me? Do I assume, without knowing anything else, that the energy of the central charge is electric, with no magnetic component at all?

 

[Dale]

But what if:
* I am the observer in the second picture.
* I do not know what the non-rotating frame is.
* I do not know to which I am rotating.
* And I see the following in second picture, except I do not know that the charge in the center which appears to be stationary is actually orbiting around the same axis I am.

Do I assume then that the charge in the center has no polar electromagnetic field when I don't know that is actually orbiting an axis that it shares with me? Do I assume, without knowing anything else, that the energy of the central charge is electric, with no magnetic component at all?

I don't know the answers to any of those, and I would be surprised if anyone else on this forum does either. That is why I said above that you should actually work the problem out, and gave you a starting place.