Pressurized Line and Rigid Tank Probem

[cwill53]

Homework Statement

Using a pressurized line, a fluid is charged in a rigid tank with volume $2m^3$. Derive the expression and calculate:
1. The internal energy $u_t$ of the fluid in that tank supposing the initial mass is $m_0=0$ , and specific enthalpy $h_i = 1670 kJ/kg.$
2. Assuming a fluid is an ideal gas, derive and calculate the tank temperature using the specific heat ratio of k = 1.67 and the initial temperature of $T_i=400 ^{\circ}C$
3. Assuming a fluid obeys ideal gas law and a flow is choked derive and calculate the tank pressure as a function of time using $\dot{m}=0.5kg/s,t=2s,k=1.67, T_i=400^{\circ}C$
Assume that charging occurs over a short period of time.

Relevant Equations

$$pV\propto RT$$
$$H=U+pV$$
$$dU=\delta Q-\delta W$$

I'm stuck on part 1 at the moment. What I had so far was

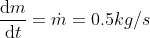
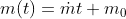
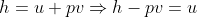
Using the ideal gas model, we have

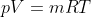
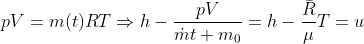
Solving these equations is reliant on the molar mass μ of the substance or the pressure p in the tank, which I don't know how to find with the given information. I sent an email to my professor and he told me to start with the first law of thermodynamics, cancel out appropriate terms and then use mass conservation taking into account that initial mass is zero. I'm not sure how to solve for the specific internal energy if that's the case. This system is isochoric if I'm not mistaken, does this mean the specific internal energy is equal to the initial specific enthalpy $h_i=1670kJ/kg$ or am I over thinking this and the specific internal energy $u_t$ is actually zero because the initial mass is zero?

 

[Chestermiller]

This is a problem in the application of the open system (control volume) version of the first law of thermodynamics. In part 1. the are asking, not for the specific internal energy of the tank contents, but the overall internal energy. The used the lower case symbol $u_t$ for the internal energy, which is confusing because lower case symbols are usually reserved for specific quantities. But certainly, if they really meant overall internal energy, it is clearly equal to 0.

Do you know the equation for the open system version of the first law of thermodynamics and how to apply it to this problem?

In part 2, they call the initial temperature 400 C, but I think they mean by this the temperature of the gas in the pressurized line.

 

[cwill53]

This is a problem in the application of the open system (control volume) version of the first law of thermodynamics. In part 1. the are asking, not for the specific internal energy of the tank contents, but the overall internal energy. The used the lower case symbol $u_t$ for the internal energy, which is confusing because lower case symbols are usually reserved for specific quantities. But certainly, if they really meant overall internal energy, it is clearly equal to 0.

Do you know the equation for the open system version of the first law of thermodynamics and how to apply it to this problem?

In part 2, they call the initial temperature 400 C, but I think they mean by this the temperature of the gas in the pressurized line.

Would I have to use the energy rate balance given by
$$\frac{dE_{cv}}{dt}=\dot{Q}_{cv}-\dot{W}_{cv}+\sum_{i}\dot{m}_i(h_i+\frac{V_i^2}{2}+gz_i)-\sum_{e}\dot{m}_e(h_e+\frac{V_e^2}{2}+gz_e)$$

I suppose I should use the one given by
$$\frac{dE_{cv}}{dt}=\dot{Q}-\dot{W}+\sum_{i}\dot{m}_i(u_i+\frac{V_i^2}{2}+gz_i)-\sum_{e}\dot{m}_e(u_e+\frac{V_e^2}{2}+gz_e)$$

and ignore the kinetic and potential energy effects. I should also ignore the $\dot{m}_e$ term.

Or maybe I should use the equation given by
$$E_{cv}(t+\Delta t)-E_{cv}(t)=Q-W+m_i(u_i+\frac{V_i^2}{2}+gz_i)-m_e(u_e+\frac{V_e^2}{2}+gz_e)$$

@Chestermiller I don't really understand how to solve part 2 if I don't know the molar mass of the gas.

 

[Chestermiller]

What happened to the h's in your original equation. They should not have changed to u's. Starting with your original equation, and neglecting kinetic energy and potential energy changes, your equation reduces to $$\frac{dU_{cv}}{dt}=\dot{Q}_{cv}-\dot{W}_{cv}+\sum_{i}\dot{m}_ih_i-\sum_{e}\dot{m}_eh_e$$Since the tank is rigid and now shaft work is being done, $\dot{W}_{cv}=0$ and since the tank and inlet are assumed insulated, $\dot{Q}=0$. In addition, the is no mass exiting the tank, but only a single mass stream entering. Therefore, the equation reduces to $$\frac{dU_{cv}}{dt}=\dot{m}_ih_i$$What to you get if you integrate this equation from time t = 0 to arbitrary time t, given that $\frac{dm}{dt}=\dot{m_i}$?

 

[cwill53]

What happened to the h's in your original equation. They should not have changed to u's. Starting with your original equation, and neglecting kinetic energy and potential energy changes, your equation reduces to $$\frac{dU_{cv}}{dt}=\dot{Q}_{cv}-\dot{W}_{cv}+\sum_{i}\dot{m}_ih_i-\sum_{e}\dot{m}_eh_e$$Since the tank is rigid and now shaft work is being done, $\dot{W}_{cv}=0$ and since the tank and inlet are assumed insulated, $\dot{Q}=0$. In addition, the is no mass exiting the tank, but only a single mass stream entering. Therefore, the equation reduces to $$\frac{dU_{cv}}{dt}=\dot{m}_ih_i$$What to you get if you integrate this equation from time t = 0 to arbitrary time t, given that $\frac{dm}{dt}=\dot{m_i}$?

I ended up getting

$$U_{cv}(2s)=\left ( 1670\frac{kJ}{kg} \right )\left ( 0.5\frac{kg}{s} \right )(2s)= 1670\frac{kJ}{kg} $$

 

[Chestermiller]

I ended up getting

View attachment 273264
$$U_{cv}(2s)=\left ( 1670\frac{kJ}{kg} \right )\left ( 0.5\frac{kg}{s} \right )(2s)= 1670\frac{kJ}{kg} $$

I get $$U_{cv}=mu=mh_{in}$$or$$u=h_{in}$$independent of t, where u is the specific internal energy of the gas within the control volume.

Based on this, what do you get in part 2?

 

[cwill53]

I get $$U_{cv}=mu=mh_{in}$$or$$u=h_{in}$$independent of t, where u is the specific internal energy of the gas within the control volume.

Based on this, what do you get in part 2?

I'm not sure how to approach this part of the problem.

 

[Chestermiller]

I'm not sure how to approach this part of the problem.

Suppose I rewrote this as $$u=u_{in}+P_{in}v_{in}$$ or $$u-u_{in}=RT_{in}$$

 

[cwill53]

Suppose I rewrote this as $$u=u_{in}+P_{in}v_{in}$$ or $$u-u_{in}=RT_{in}$$

This makes sense, but how do I know which specific gas constant to use if I don't know the molar mass of the gas? Or is the temperature zero?

 

[Chestermiller]

This makes sense, but how do I know which specific gas constant to use if I don't know the molar mass of the gas?

This also works for moles.

 

[cwill53]

This also works for moles.

Is there a difference between $u$ and $u_{in}$?

 

[Chestermiller]

Is there a difference between $u$ and $u_{in}$?

u is at T and uin is at Tin

 

[cwill53]

u is at T and uin is at Tin

I'm sorry, but I still don't understand how I can solve the equation without knowing the molar mass of this gas, if $R=\frac{\bar{R}}{\mu }$.

 

[Chestermiller]

$$C_v(T-T_{in})=RT_{in}$$where Cv is the molar heat capacity at constant volume and R is the universal gas constant.

 

[cwill53]

$$C_v(T-T_{in})=RT_{in}$$where Cv is the molar heat capacity at constant volume and R is the universal gas constant.

What is u(T) and h(T)? I have
$$u(T)-u(T_{i})=c_v(T-T_i)=RT_i$$
$$h(T)-h(T_i)=c_p(T-T_i)=RT_i+R(T-T_i)$$

 

[Chestermiller]

What is u(T) and h(T)? I have
$$u(T)-u(T_{i})=c_v(T-T_i)=RT_i$$
$$h(T)-h(T_i)=c_p(T-T_i)=RT_i+R(T-T_i)$$

I don’t understand what you are asking. Just solve for T . u(T) is the molar internal energy and h(T) is the molar enthalpy of the tank contents.

 

[cwill53]

I don’t understand what you are asking. Just solve for T .

We only have information on $u(T_i)$ and $h(T_i)$ right? I don't understand how to solve this without knowing $u(T)$ and $h(T)$.

 

[Chestermiller]

Are you saying you don't know how to solve this equation
$$C_v(T-T_i)=RT_i$$ for T?

 

[cwill53]

Are you saying you don't know how to solve this equation
$$C_v(T-T_i)=RT_i$$ for T?

I know how to solve it, but I don't know the values for each variable. We have $c_v$ but I don't know the numerical value of it. All I know is that k=1.67.

 

[Chestermiller]

I know how to solve it, but I don't know the values for each variable. We have $c_v$ but I don't know the numerical value of it. All I know is that k=1.67.

How is Cp related to Cv, and what is the definition of k?

 

[cwill53]

How is Cp related to Cv, and what is the definition of k?

$$k=\frac{c_p}{c_v};c_p=c_v+R$$

I see now that
$$T=(1+\frac{R}{c_v})T_i=kT_i$$

@Chestermiller I'm struggling to solve the third part.

 

[cwill53]

@Chestermiller For part 3, I keep going in circles trying to figure out a numerical value of R.

We have
$$k=\frac{c_p}{c_v}=1.67$$
$$R=0.67c_v\Leftrightarrow 1.4925R=c_v$$
$$0.401197c_p=R\Leftrightarrow 2.49254R= c_p$$
Using the ideal gas equation, I wrote
$$pV=\dot{m}tR(kT_i)=m(t)R(1124.1605K)$$

 

[Chestermiller]

@Chestermiller For part 3, I keep going in circles trying to figure out a numerical value of R.

We have
$$k=\frac{c_p}{c_v}=1.67$$
$$R=0.67c_v\Leftrightarrow 1.4925R=c_v$$
$$0.401197c_p=R\Leftrightarrow 2.49254R= c_p$$
Using the ideal gas equation, I wrote
$$pV=\dot{m}tR(kT_i)=m(t)R(1124.1605K)$$

R = 8.314 J/mole-K

 

[cwill53]

R = 8.314 J/mole-K

This is what I ended up writing, going from the last part of the problem, and substituting to find the temperature.
Substituting, we have:

For part 3, we have to find the tank pressure as a function of time using the ideal gas equation of state,

where the specific gas constant R is defined as, with μ being the molar mass of the gas,

Using the available information, we can write the ideal gas law for this problem as

From the definition of heat capacity at constant pressure and specific heat capacity at constant pressure, we have

For an ideal gas, specific heat capacity is a function of temperature alone, that is

for an ideal gas. After separating variables, we can obtain infinitesimal and finite difference forms of this equation:

From this, we can get a numerical value of cp(T), assuming that h(T)-h(Ti)=1670 kJ/kg:

Using this we can attempt to get a numerical value for the specific gas constant R. Remembering the definition of specific heat capacity at constant pressure cp(T) = cv(T)+R, we have

Solving numerically for R, we have

Defining pressure p as a function of time t,

we have, after rearrangement of the ideal gas equation of state,
$$P(t)=\frac{\dot{m}tRkT_i}{V}$$
At a time t of 2 seconds, we have
$$P(2s)=\frac{(0.5\frac{kg}{s})(2s)(1.4856\frac{kJ}{kg\cdot K})(1.67)(673.15K)}{2m^3}=835.026\frac{kJ}{m^3}=835.026kPa$$

 

[Chestermiller]

I don't know whether any of this is correct. I can see that, to do the calculation for part 3, you need to know the molecular weight. However, I don't understand why you used 400 C as the reference temperature for zero enthalpy. If that is what they mean by the condition of zero enthalpy, then I get a molecular weight of 5.6 g/mole, which is non-integer and doesn't make sense.

 

[cwill53]

I don't know whether any of this is correct. I can see that, to do the calculation for part 3, you need to know the molecular weight. However, I don't understand why you used 400 C as the reference temperature for zero enthalpy. If that is what they mean by the condition of zero enthalpy, then I get a molecular weight of 5.6 g/mole, which is non-integer and doesn't make sense.

I ended up revising my answer and assuming that the specific heats do not vary over this temperature range as these are ideal gases. Doing this I assumed that

$$h_i=c_p(T)T_i$$
and got a molar mass of $8.55\frac{kg}{kmol}$. I honestly am clueless at this point. Maybe it's an imaginary substance lol. Lithium hydride is not a gas. Hydrogen and helium can't bond with each other. Helium doesn't form diatomic molecules. Hydrogen doesn't form octoatomic configurations on its own. So I don't know ; )

 

[Chestermiller]

The value of k indicates a monoatomic gas, but the MW of helium is 4 and the MW of neon is 20.

 

[cwill53]

The value of k indicates a monoatomic gas, but the MW of helium is 4 and the MW of neon is 20.

The gas must certainly be made up then.