- #1
ashah99
- 60
- 2
- Homework Statement
- Problem shown below. Various topics related to the joint pdf and RVs
- Relevant Equations
- Equations used are shown in working attempt below.
Hello all, I would like to check my understanding and get some assistance with last part of the following question, please.
For part (d), would I use f(x | y) = f(x, y) / f(y) ?
Problem statement:

My attempt at a solution, not too confident in my set-up for part (d). I drew a sketch of the region of integration.
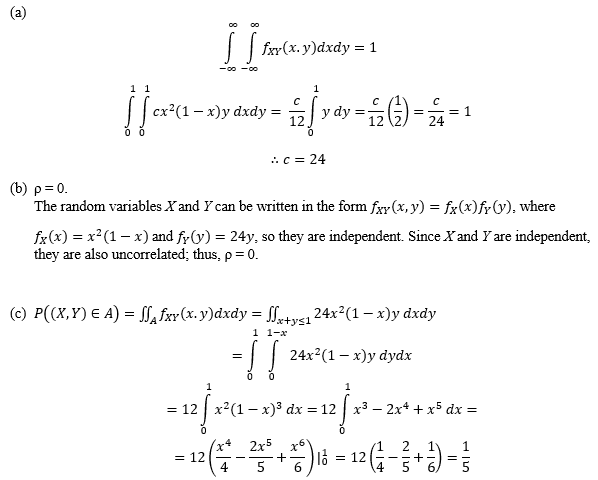
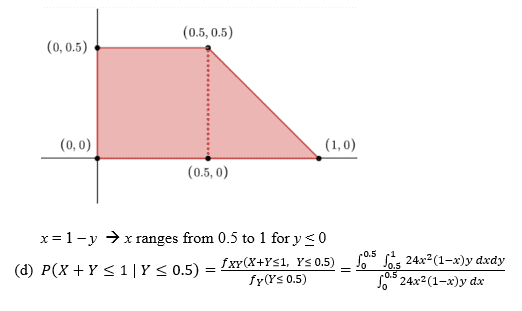
For part (d), would I use f(x | y) = f(x, y) / f(y) ?
Problem statement:
My attempt at a solution, not too confident in my set-up for part (d). I drew a sketch of the region of integration.