Problem involving two pulleys

[issacnewton]

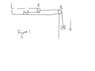
Mass m1 on a frictionless horizontal table is connected
to mass m2 by means of a very light pulley P1 and a light
fixed pulley P2 as shown in Figure 1. (a) If a1 and a2
are the accelerations of m1 and m2 , respectively, what is
the relationship between these accelerations? Express
(b) the tensions in the strings and (c) the accelerations
a1 and a2 in terms of the masses m1 and m2 and g.

Now I set up following equations

m[2]g - T[2] = m[2]a[2]

where a[2] is downward acceleration of m[2].

Also T[1]=m[1](a[r]+a[2])

where a[r] is acceleration of m[1] relative to P1. I have attached the Figure 1.
Now I have no idea how to proceed. I have to solve for T[1], T[2] and a[2] and
a[1]=a[r]+a[2] in terms of m[1], m[2] and g. Please help

 

[earlofwessex]

if the pulley moves with acceleration a₂, and assuming that the rope connecting M₁ to the wall doesn't stretch, what else can you say about a₁?

 

[issacnewton]

can i say that a1 is 2 times a2 ?

 

[earlofwessex]

yup, you got it

 

[issacnewton]

but that still doesn't help solve a1,a2 and T1 , T2 in terms of m1, m2 and g. how do i
do that ?

 

[method_man]

but that still doesn't help solve a1,a2 and T1 , T2 in terms of m1, m2 and g. how do i
do that ?

You have got the solution http://www.ux1.eiu.edu/~cfadd/1350/Hmwk/Ch05/Ch5.html" . Look at the example 5.2. Scroll down for the solution.

 

[issacnewton]

method_man, i looked at the given solution. thanks for that. but i see one problem in the solution given. at one point they say
2T1=T2 at the pulley P1. But pulley P1 is accelerating to the right with acceleration a2. So how can we equate the forces
acting on it in the left direction to the forces acting on it in the right direction. If 2T1=T2 , pulley P1 would either be at rest
or move with constant velocity.

thanks

 

[method_man]

Yes, that's a good question. But in your problem you said that P1 is a very light pulley.
So therefore, you have two T1 forces looking left and T2 force looking right. If P1 would have some significant mass then you would have additional force which is equal to pulley mass multiplied with a₁.

 

[issacnewton]

i think its better to let pulley P1 have some mass m3. and we can set up the equation
T2 - 2T1 = m3*a2. and then we can apply the limit that m3 tend to zero. in this way we can get the equation we want (which is T2 = 2*T1) without compromising any physics.
so the above equation is true in the limit that m3 tend to zero. i think i feel comfortable
in this way of thinking about it. actually this is what i thought when i began with the problem but then the fact that pulley P1 is nearly massless stumped me and I couldn't get around that and come up with an equation. thanks again to both of you.

Issac Newton