Problem on the transfer of heat into different materials

[lemonbrook]

Hi all,

1. The problem statement

A copper specimen, initially at 293K, is immersed in a bath of liquid salt at 773K. The bath is agitated and the heat transfer at the surface of the metal is effectively perfect. A temperature of 723K is measured at 5mm below the surface of the metal item after 3 seconds. Estimate the depth below the surface at which a temperature of 723K would be reached in 3 seconds if the specimen were made of titanium alloy.

Copper

Thermal Conductivity = 380 W m^-1 K^-1
Specific Heat Capacity = 390 J kg^-1 K^-1
Density - 8900 kg m^-3

Titanium

Thermal Conductivity = 6 W m^-1 K^-1
Specific Heat Capacity = 500 J kg^-1 K^-1
Density - 4500 kg m^-3

Homework Equations

This equation wasn't given in the question but seems to be relevant.

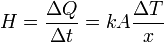
where

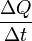is the rate of heat flow, k is the thermal conductivity, A is the total cross sectional area of conducting surface, ΔT is temperature difference, and x is the thickness of conducting surface separating the 2 temperatures.

The Attempt at a Solution

I'm very confused as to how to approach this problem. I first attempted to rearrange the equation for Area, but I would also need to have ΔQ which would require a mass to calculate. Could I just use and arbitrary volume for both components and use the density to calculate a mass?

Thanks

 

[Mapes]

Hi lemonbrook, welcome to PF. A common way of estimating the required time for a temperature change to propagate a distance L is L^2/D, where D is the material's http://en.wikipedia.org/wiki/Thermal_diffusivity" .

 

[lemonbrook]

That it!

Thanks very much!