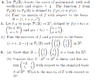shaon0
- 48
- 0
Homework Statement
See Attachment.
The Attempt at a Solution
For the first two questions, I know I have to sub in values for a and b. But, I'm not sure what the output matrix is.
The 3rd q, to prove B is Basis for R^3. I just have to row reduce [(1,5);(1,6)] to get [(1,0);(0,1)] right? But like before, I don't know how to do b).
Any help is appreciated.