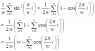You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Proving Discrete Sum Equation - Step-by-Step Guide and Tips
Physics news on Phys.org
Dick
Science Advisor
Homework Helper
- 26,254
- 623
Start by using a double angle formula to express sin(x)^2 in terms of cos(2x). Now get started.
darkfeffy
- 17
- 0
Thinking it might just be an assumption that this last term is exceedingly small compared to the first.
Dick
Science Advisor
Homework Helper
- 26,254
- 623
darkfeffy said:Thinking it might just be an assumption that this last term is exceedingly small compared to the first.
Do you know Euler's formula, e^(ix)=cos(x)+i*sin(x) (i the imaginary unit, not the integer index)? That would let you treat the sum of the cos term as the real part of the sum of a geometric series. And no, there's no approximation here. The cos part really does sum to zero.
Last edited:
- 15,524
- 769
You are correct in that the term is exceedingly small (zero is an exceedingly small number). You are incorrect in that is an assumption.darkfeffy said:Thinking it might just be an assumption that this last term is exceedingly small compared to the first.
darkfeffy
- 17
- 0
Thanks Dick.Dick said:Do you know Euler's formula, e^(ix)=cos(x)+i*sin(x) (i the imaginary unit, not the integer index)? That would let you treat the sum of the cos term as the real part of the sum of a geometric series. And no, there's no approximation here. The cos part really does sum to zero.
darkfeffy
- 17
- 0
Thanks DH for your brilliant reply which really doesn't add much information :-)D H said:You are correct in that the term is exceedingly small (zero is an exceedingly small number). You are incorrect in that is an assumption.
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 4
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 1K
- Replies
- 28
- Views
- 2K
- Replies
- 6
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math