adjacent
Gold Member
- 1,552
- 62
One rule of circle theorems is,a line drawn from center to the mid-point of a chord cuts the cord at 90°.
What's the proof?
It's true that two radius and a chord creates an isosceles triangle.
So,
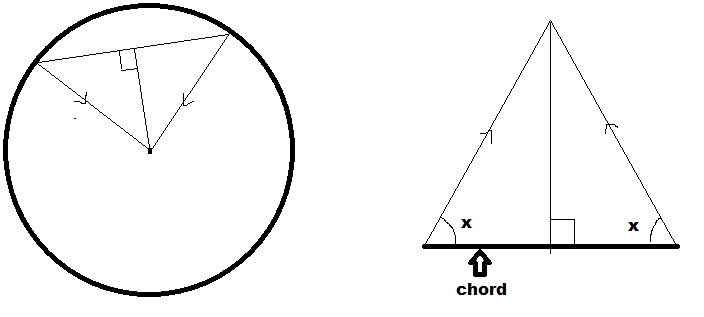
How can I prove that in an isosceles triangle,a line drawn from the vertex angle to the mid-point of the base side cuts the side at 90°?
What's the proof?
It's true that two radius and a chord creates an isosceles triangle.
So,
How can I prove that in an isosceles triangle,a line drawn from the vertex angle to the mid-point of the base side cuts the side at 90°?
Attachments
Last edited: