Solving Pulley and Platform Homework w/ Acceleration

In summary: You're just trying to push it in the opposite direction.You are applying the force downwards! You're just trying to push it in the opposite direction.
  • #1
judas_priest
174
0

Homework Statement



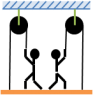
Two construction workers each of mass m raise themselves on a hanging platform using pulleys as shown above. If the platform has a mass of 0.5m, the initial distance between the pulleys and the platform is d, and the workers each pull with a force f on the ropes, what is the acceleration a of the workers? Assume the pulleys and ropes are massless.

Homework Equations





The Attempt at a Solution



Forces on one Man:
FME (weight of the man),
The normal force NMP (contact of the man with the platform),
The tension force FMR (the response force that the rope applies to the man).
The force applied by 2 men pointing down

For the platform:
FPE (weight of the platform),
NPM (force on the platform due to the man, it is the pair of NMP) and remember you have two of this because you have 2 men,
T and T: The two tensions acting on the platform due to the ropes
 

Attachments

  • Pulley Platform.png
    Pulley Platform.png
    1.3 KB · Views: 681
Physics news on Phys.org
  • #2
I would consider men+platform as one system. This reduces the number of forces involved.

What did you do after listing all those forces?
 
  • #3
Eliminated Normal force. What answer do you get? I tried doing it by considering them as a one system too. Still stuck.
 
  • #4
mfb said:
I would consider men+platform as one system. This reduces the number of forces involved.

What did you do after listing all those forces?

Considering them as one system:

2N downwards
2N upwards
2mg + .5 mg downwards
2f downwards (force applied by men)
2f upwards. (The tension in the strings attached to the platform)
2t upwards. (the tension in the strings held by men)

Where am I going wrong?
 
  • #5
2f downwards (force applied by men)
They do not apply a downwards force on the pulley/men system.
2f upwards. (The tension in the strings attached to the platform)
2t upwards. (the tension in the strings held by men)
Where is the difference between f and t?

The other forces look good.
 
  • #6
mfb said:
They do not apply a downwards force on the pulley/men system.
Where is the difference between f and t?

The other forces look good.

But the question says they pull down with a force f. What are the correct forces?
also, is there a difference between f and t in this case?
 
  • #7
They pull the rope down, and themself up.
also, is there a difference between f and t in this case?
That was my question to you. Can the rope tension be different at both sides?
 
  • #8
mfb said:
They pull the rope down, and themself up.
That was my question to you. Can the rope tension be different at both sides?

Okay, so tension and force are the same in this case. Can you please list out all the forces?
 
  • #9
For the two men combined:
[tex] 2N - 2F - 2Mg = 2Ma [/tex]
For the platform
[tex] 2f -.5Mg - 2N = .5Ma [/tex]

Is that right?
 
  • #10
judas_priest said:
For the two men combined:
[tex] 2N - 2F - 2Mg = 2Ma [/tex]
Is that right?

Why the minus sign in -2F here?
 
  • #11
Because they're pulling it down.
Here's another way I did it in:
Forces on 2 men
tension upwards
normal upwards
weight downwards

Forces on platform:
normal downwards
weight downwards

I've ignored the forces applied by the two men to pull the string down, because they get balanced by the forces on platform pointing up
 
  • #12
F points upwards for the men, as I mentioned before. They are pulling the rope down, so they are pulling themself up.
Apart from that, post 9 is right.

I've ignored the forces applied by the two men to pull the string down, because they get balanced by the forces on platform pointing up
That does not work.
 
  • #13
But aren't they trying to pull it down? How would it point upwards?
And F gets balanced by the force on platform. Don't they?
 
  • #14
mfb said:
They are pulling the rope down, so they are pulling themself up.
Apart from that, post 9 is right.

That does not work.

Why not? They are reaction forces after all? How does F point upwards for men when they're applying force downwards.
Also, Isn't tension upwards?
 
  • #15
[tex] 2N + 2F - 2Mg = 2Ma [/tex]

[tex] 2F -.5Mg - 2N = .5Ma [/tex]

Solving them, this is what I get:

[tex]4F - 25m = 2.5Ma [/tex]

Is that correct?
 
  • #16
judas_priest said:
But aren't they trying to pull it down?
Did you ever try to push a rope? Did it work?
You can only pull it, and get a positive tension in it.
They are "trying" to pull at the anchor on the top of the building. As this anchor feels a force downwards, they feel a force upwards (action/reaction).

Also, Isn't tension upwards?
Exactly, tension pulls them upwards.

Is that correct?
If you add the missing decimal point, yes.
 
  • #17
mfb said:
Did you ever try to push a rope? Did it work?
You can only pull it, and get a positive tension in it.
They are "trying" to pull at the anchor on the top of the building. As this anchor feels a force downwards, they feel a force upwards (action/reaction).

Exactly, tension pulls them upwards.

If you add the missing decimal point, yes.

I'm confused. If I'm pulling the rope, am I not applying the force downwards? Of course, it's upwards on the platform. And isn't the equation incomplete without tension?
Also, I did add the decimal points.
 
  • #18
I got the answer, but can someone explain to me the working of this problem? I haven't understood it.
I just got the answer by blindly following the posts
 
  • #19
mfb said:
If you add the missing decimal point, yes.
I think judas_priest has substituted g = 10.
judas_priest said:
If I'm pulling the rope, am I not applying the force downwards?
Yes, downwards on the rope, so the rope is applying the same force upwards on you.
The quick way to solve this problem is to consider the forces pulling upwards the pulleys. What do these add up to?
 
  • #20
haruspex said:
I think judas_priest has substituted g = 10.

Yes, downwards on the rope, so the rope is applying the same force upwards on you.
The quick way to solve this problem is to consider the forces pulling upwards the pulleys. What do these add up to?

Okay, got it. Thanks a lot!
 
  • #21
im trying to figure this out but I am really confused where did the 2N come from?
 
  • #22
lollikey said:
im trying to figure this out but I am really confused where did the 2N come from?
As in post #10? N is the normal force from the platform on each man. Total = 2N.
 
  • #23
ohh okay ! thank you ! I thought it was that but I got confused because on a later post it was said there is no normal force
 
  • #24
My problem :Two construction workers each of mass m raise themselves on a hanging platform using pulleys as shown above. If the platform has a mass of 5m and the workers each pull with a force f on the ropes, what is the acceleration a of the workers? Assume the pulleys and ropes are massless.

so would the forces be

2N up
2N down
7mg down
4f up

?

and you would add all of them up and equal to mass*acceleration (ma)?
 
Last edited:
  • #25
lollikey said:
My problem :Two construction workers each of mass m raise themselves on a hanging platform using pulleys as shown above. If the platform has a mass of 5m and the workers each pull with a force f on the ropes, what is the acceleration a of the workers? Assume the pulleys and ropes are massless.

so would the forces be

2N up
2N down
7mg down
4f up

?

and you would add all of them up and equal to mass*acceleration (ma)?
Yes, if the m in the last line represents the total mass, not the given m.
 
  • #26
so the equation would be 2N-2N+2f+2f+7mg=7mga
to find acceleration it would be (4f+7mg)/7mg= a ?
 
  • #27
it marked it wrong. I am soo confused! what am I doing wrong?
 
  • #28
lollikey said:
so the equation would be 2N-2N+2f+2f+7mg=7mga
7mga? That's multiplying two accelerations together.
 
  • #29
but I thought that since both men have a mass of m and the platforms mass is 5m the total mass would be 7m
so would the formula just be 2N-2N+2f+2f+7mga = 7ma ??
 
  • #30
I got it ! the answer is (4f-7mg) / 7m
 
  • #31
lollikey said:
I got it ! the answer is (4f-7mg) / 7m
Good show.
 
  • #32
Well, I can't understand why there are 4f and not 2f. I thought it was mechanical advantage but these pulleys are fixed to the ceiling, aren't they? I am obviously missing something.
 
  • #33
Poetria said:
Well, I can't understand why there are 4f and not 2f. I thought it was mechanical advantage but these pulleys are fixed to the ceiling, aren't they? I am obviously missing something.
Draw a line across just below the pulleys. How many ropes cross that line? What is the tension in each?
 
  • Like
Likes Poetria
  • #34
I see. There are four ropes and each of them has tension f.
 
  • #35
Poetria said:
I see. There are four ropes and each of them has tension f.
Right.
 
  • Like
Likes Poetria
<h2>1. How do I determine the acceleration of a pulley and platform system?</h2><p>To determine the acceleration of a pulley and platform system, you will need to use Newton's Second Law of Motion, which states that the net force acting on an object is equal to its mass multiplied by its acceleration. You will also need to consider the forces acting on the system, such as tension and friction, and use equations of motion to solve for the acceleration.</p><h2>2. What is the relationship between acceleration and mass in a pulley and platform system?</h2><p>The relationship between acceleration and mass in a pulley and platform system is inverse. This means that as the mass of the system increases, the acceleration decreases, and vice versa. This is because the mass of the system affects the net force acting on it, which in turn affects the acceleration.</p><h2>3. How do I account for friction in my calculations for a pulley and platform system?</h2><p>To account for friction in your calculations for a pulley and platform system, you will need to identify the surfaces where friction is present and use the coefficient of friction to calculate the frictional force. This force should then be included in your equations of motion to accurately determine the acceleration of the system.</p><h2>4. Can I assume that the pulley and platform system is in equilibrium when solving for acceleration?</h2><p>No, you cannot assume that the pulley and platform system is in equilibrium when solving for acceleration. In most cases, there will be an unbalanced force acting on the system, which will result in an acceleration. However, if the system is at rest and not moving, then it can be assumed to be in equilibrium.</p><h2>5. What are some common mistakes to avoid when solving pulley and platform homework with acceleration?</h2><p>Some common mistakes to avoid when solving pulley and platform homework with acceleration include not considering all the forces acting on the system, not using the correct equations of motion, and not properly accounting for friction. It is also important to double-check your calculations and units to ensure accuracy in your answers.</p>

1. How do I determine the acceleration of a pulley and platform system?

To determine the acceleration of a pulley and platform system, you will need to use Newton's Second Law of Motion, which states that the net force acting on an object is equal to its mass multiplied by its acceleration. You will also need to consider the forces acting on the system, such as tension and friction, and use equations of motion to solve for the acceleration.

2. What is the relationship between acceleration and mass in a pulley and platform system?

The relationship between acceleration and mass in a pulley and platform system is inverse. This means that as the mass of the system increases, the acceleration decreases, and vice versa. This is because the mass of the system affects the net force acting on it, which in turn affects the acceleration.

3. How do I account for friction in my calculations for a pulley and platform system?

To account for friction in your calculations for a pulley and platform system, you will need to identify the surfaces where friction is present and use the coefficient of friction to calculate the frictional force. This force should then be included in your equations of motion to accurately determine the acceleration of the system.

4. Can I assume that the pulley and platform system is in equilibrium when solving for acceleration?

No, you cannot assume that the pulley and platform system is in equilibrium when solving for acceleration. In most cases, there will be an unbalanced force acting on the system, which will result in an acceleration. However, if the system is at rest and not moving, then it can be assumed to be in equilibrium.

5. What are some common mistakes to avoid when solving pulley and platform homework with acceleration?

Some common mistakes to avoid when solving pulley and platform homework with acceleration include not considering all the forces acting on the system, not using the correct equations of motion, and not properly accounting for friction. It is also important to double-check your calculations and units to ensure accuracy in your answers.

Similar threads

Newton's Second Law (Pulley Sustem)
    • Introductory Physics Homework Help
Replies
3
Views
791
Mechanics Pulley Platform Problem
    • Introductory Physics Homework Help
Replies
13
Views
3K
Olympiad dynamics problem with 3 masses and a pulley
    • Introductory Physics Homework Help
Replies
17
Views
1K
Analyzing Forces in a Platform and Pulley System
    • Introductory Physics Homework Help
Replies
5
Views
3K
Solve Pulley Problem: Frustrated After Weeks of Trying
    • Introductory Physics Homework Help
Replies
4
Views
1K
Rope Swing, starting in tension vs slack
    • Mechanical Engineering
Replies
3
Views
207
Experimental Design: Pulley and Mass Hangers
    • Introductory Physics Homework Help
Replies
30
Views
1K
Calc Forces on Pulleys: 200N, 300N Masses, No Friction
    • Introductory Physics Homework Help
Replies
1
Views
982
Wordy Physics on Forces, Pulleys, and Friction
    • Introductory Physics Homework Help
Replies
5
Views
4K
Defining equilibrium and movement in pulley arrangements
    • Introductory Physics Homework Help
Replies
8
Views
1K

Hot Threads

Recent Insights

Back
Top