AliGh
- 64
- 1
Thread moved from the technical Physics forums, so ho HH Template is shown
Hi today the teacher showed us analyzing forces in a system he showed them on easy problems
But at the end of the class he gave us this question to solve
Its not homework because its way beyond what he taught
The base moves without friction on surface
So i want to find a3 and theta and a of 2 and 1
How should i do this ? Where should i start from ?
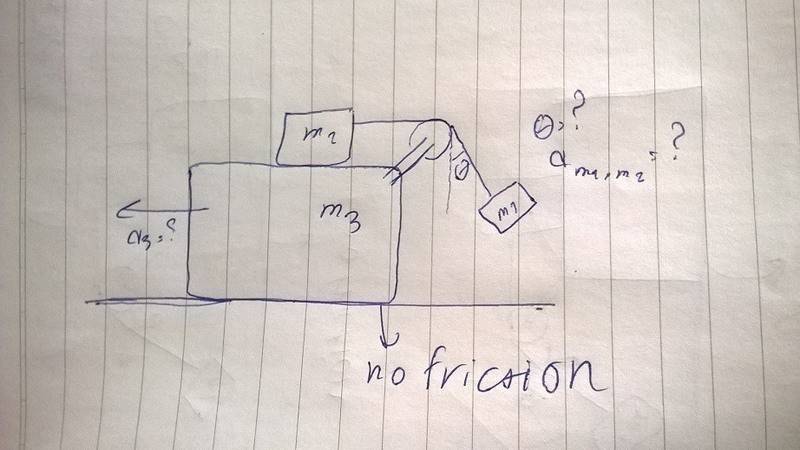
But at the end of the class he gave us this question to solve
Its not homework because its way beyond what he taught
The base moves without friction on surface
So i want to find a3 and theta and a of 2 and 1
How should i do this ? Where should i start from ?