Pulley system, find the acceleration and tension

[Davidllerenav]

Homework Statement

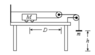
Given the picture:

• Make the free body diagrams of each body and the pulley. Remember that there are two different strings therefore there are two different tensions.
• Assuming that the mobile of mass M starts from rest and has a displacement D at a time t, and the bodywith mass m falls a height h at the same time, calculate the accelerations of the mobile a_1 and the body a_2 (Note: Use only cinematics).
• Assuming that the accelerations of the bodies are known, calculate the tensions in the strings, and the coefficient of friction between the mobile and the table. Despise the pulley mass and friction between pulleys and rope.
  

Homework Equations

Kinematics equations.

The Attempt at a Solution

Ok, So for the first one, I made the diagrams of each body like this. Is it correct?

For the second one, it says that the mobile of mass M starts from rest, so $v_0M=0$, and $v_M=at$. The displacement would be $D=\frac{at^2}{2}+D_0$, so the acceleration would be $a_1= \frac{V_M}{t} = \frac{2D}{t^2} + D_0$.
Now, for the body with mass m I set the inicial speed as $0$, so $v_0m=0$, thus $V_m=-gt$. The Fall would be $F=h-\frac{gt^2}{2}. Thus$g= -\frac{v_m}{t} = h-\frac{2F}{t^2}. Am I correct?

For the third one, I don't know what to do. Pleas help me.

 

[haruspex]

It's a bit hard to read the details on your diagrams, but the tensions don’t look right.
If a string passes over a pulley, and the pulley is considered massless and frictionless, what can you say about the tensions in the two segments of string?

 

[Davidllerenav]

It's a bit hard to read the details on your diagrams, but the tensions don’t look right.
If a string passes over a pulley, and the pulley is considered massless and frictionless, what can you say about the tensions in the two segments of string?

That they are the same.

 

[haruspex]

That they are the same.

But that does not seem to be what either of your pulley diagrams show. As I wrote, they are hard to read though.

 

[Davidllerenav]

But that does not seem to be what either of your pulley diagrams show. As I wrote, they are hard to read though.

Yes, sorry I think I labelled them wrong. But I think that on Pulley 1, both tensions are the same, right? On pulley 2 the tensions on the left are the same and the one on the right is the same as the tension on pulley 1. The tension that mass M feels is the same as the left ones on pulley 2 and the tension that mass 2 feels is the same as pulley 1, right?

 

[haruspex]

Yes, sorry I think I labelled them wrong. But I think that on Pulley 1, both tensions are the same, right? On pulley 2 the tensions on the left are the same and the one on the right is the same as the tension on pulley 1. The tension that mass M feels is the same as the left ones on pulley 2 and the tension that mass 2 feels is the same as pulley 1, right?

Yes, that all sounds fine.

Your equation for D is ok, but you can set D⁰=0. We are only concerned with the displacement.

The Fall would be $F=h-\frac{gt^2}{2}$. Thus $g= -\frac{v_m}{t} = h-\frac{2F}{t^2}$. Am I correct?
.

what forces act on m?

 

[Davidllerenav]

what forces act on m?

Tension and gravity.

 

[Orodruin]

Note that the FBD of pulley 1 is not correct. If those were the only forces acting on it it would accelerate down and to the left. However, this is irrelevant to the problem itself as what you need is the relation between the tensions in the string going left and that going down. This is a very common mistake that you should aim to avoid. Even though it does not matter in this problem, there are problems where it will matter.

 

[Davidllerenav]

Note that the FBD of pulley 1 is not correct. If those were the only forces acting on it it would accelerate down and to the left. However, this is irrelevant to the problem itself as what you need is the relation between the tensions in the string going left and that going down. This is a very common mistake that you should aim to avoid. Even though it does not matter in this problem, there are problems where it will matter.

There should be a force pointing up and a force pointgin right, is it correct? But what are those forces?

 

[Orodruin]

But what are those forces?

Look at the figure. What other forces on the pulley are available that you did not draw in your diagram? (It does not need to be two separate forces, it is sufficient to have one force pointing up and right.)

 

[haruspex]

Tension and gravity.

So will the acceleration be g?
Note that fir this part of the question you are told to take its a celeration as just a₂.

 

[Davidllerenav]

Look at the figure. What other forces on the pulley are available that you did not draw in your diagram? (It does not need to be two separate forces, it is sufficient to have one force pointing up and right.)

The only one I can think of is the one provided by that support.

 

[Davidllerenav]

So will the acceleration be g?
Note that fir this part of the question you are told to take its a celeration as just a₂.

Oh, so I just need to change the g to a $a_2$?

 

[haruspex]

The only one I can think of is the one provided by that support.

That's what the support is for, to supply whatever force is needed to keep it in place.

 

[haruspex]

Oh, so I just need to change the g to a $a_2$?

Yes.

 

[Davidllerenav]

That's what the support is for, to supply whatever force is needed to keep it in place.

So it wold provide a force that isn't pointing up or right, but I need to find it's components, right?

 

[haruspex]

So it wold provide a force that isn't pointing up or right, but I need to find it's components, right?

You know that it has to balance the two tension forces, so which direction must it point?

 

[Davidllerenav]

You know that it has to balance the two tension forces, so which direction must it point?

It must point up and right.

 

[haruspex]

It must point up and right.

At what angle?

 

[Davidllerenav]

At what angle?

$45$ degrees,right?

 

[Orodruin]

Right, it is a side-track to your problem and you do not need to care about it here though. However, as I said, there are problems where the support is attached to some mass that is movable and then it will matter so it is good to get this right from the beginning. I suggest you move on with the rest of this problem now and don't spend too much time on the support forces, but being aware of it is good practice and sometimes necessary.

 

[haruspex]

$45$ degrees,right?

Yes.

 

[Davidllerenav]

Right, it is a side-track to your problem and you do not need to care about it here though. However, as I said, there are problems where the support is attached to some mass that is movable and then it will matter so it is good to get this right from the beginning. I suggest you move on with the rest of this problem now and don't spend too much time on the support forces, but being aware of it is good practice and sometimes necessary.

Ok, thanks. I will have a test about this tomorrow on my lab class, so maybe the teacher wants to see the support forces. But one question, would't that change the sum of forces?

 

[Orodruin]

Ok, thanks. I will have a test about this tomorrow on my lab class, so maybe the teacher wants to see the support forces. But one question, would't that change the sum of forces?

It is the only thing that makes it possible for your pulley's centre of mass to not accelerate, so yes. Without the support forces, the forces on the pulley cannot be equal to zero unless the tension is zero. The equality of the tensile forces is due to torque balance (assuming that the pulley is mass- and frictionless), because the support force is acting through the pulley centre of mass, but without the support force the pulley centre of mass would accelerate (which goes against the entire idea that it is fixed in place).

If I was your teacher and asked you to draw the forces on the pulley I would deduct points for not drawing the support force.

 

[Davidllerenav]

Yes.

Ok, thanks. Sorry to ask here, but I posted I question before this one about circular motion, can you help me with it?

 

[Davidllerenav]

It is the only thing that makes it possible for your pulley's centre of mass to not accelerate, so yes. Without the support forces, the forces on the pulley cannot be equal to zero unless the tension is zero. The equality of the tensile forces is due to torque balance (assuming that the pulley is mass- and frictionless), because the support force is acting through the pulley centre of mass, but without the support force the pulley centre of mass would accelerate (which goes against the entire idea that it is fixed in place).

If I was your teacher and asked you to draw the forces on the pulley I would deduct points for not drawing the support force.

Ok. But one question. The third part says that there is acceleration, so what happens to those forces?

 

[Orodruin]

Ok. But one question. The third part says that there is acceleration, so what happens to those forces?

There is no (linear) acceleration of the pulley. It is locked into place by the support.

 

[Davidllerenav]

There is no (linear) acceleration of the pulley. It is locked into place by the support.

Oh, sorry I confused it witht he mass. So the pully is at rest always. The other one is too right?

 

[Orodruin]

Oh, sorry I confused it witht he mass. So the pully is at rest always. The other one is too right?

No, the other pulley will have to move. If it did not move the hanging mass would not be able to move. However, it is supposedly massless in this problem. Note that there is no separate support keeping it in place.

 

[Davidllerenav]

No, the other pulley will have to move. If it did not move the hanging mass would not be able to move. However, it is supposedly massless in this problem. Note that there is no separate support keeping it in place.

So it would move to the right, pulling the mobile and letting the hanging mass to fall?

 

[Orodruin]

It would be more accurate to say it would accelerate to the right due to the pull of the hanging mass. Of course, if the system starts at rest this will lead to it moving to the right.

 

[Davidllerenav]

It would be more accurate to say it would accelerate to the right due to the pull of the hanging mass. Of course, if the system starts at rest this will lead to it moving to the right.

I see. Ok, I wrote the sum of forces like this:

• Mobile with mass M: $T_1-F_r=M\cdot a_1\Rightarrow T_1-\mu N = M\cdot a_1 \Rightarrow T_1=\mu Mg+M\cdot a_1\Rightarrow T_1=M(\mu g+a_1)$
• Hanging body with mass m: Since it moves down, the force of gravity is bigger than the tension, thus $F_g-T_2=m\cdot a_2\Rightarrow mg-T_2=m\cdot a_2\Rightarrow T_2=m(g-a_2)$

Is it correct?

 

[Orodruin]

No, you mixed up $T_1$ and $T_2$ from one step to the next. It may seem petty, but you have done this several times in this thread alone and you need to take better care with this or you will make mistakes that are relatively easy to avoid.

 

[Davidllerenav]

No, you mixed up $T_1$ and $T_2$ from one step to the next. It may seem petty, but you have done this several times in this thread alone and you need to take better care with this or you will make mistakes that are relatively easy to avoid.

Sorry, I fixed it now. I'll try to be como careful. Now that it is fixed, is it correct?

 

[Orodruin]

Yes, but you need to find a relation between $T_1$ and $T_2$ to completely solve your system. Can you imagine where you can get such a relation from?

 

[Davidllerenav]

Yes, but you need to find a relation between $T_1$ and $T_2$ to completely solve your system. Can you imagine where you can get such a relation from?

I guess I need to make both of them somehow equal. But I don't know where I can get that relation from. I guess that since there are two $T_1$ tensions on the right side of the middle pulley, then the second tension must be half $T_1$?

 

[Orodruin]

I guess I need to make both of them somehow equal. But I don't know where I can get that relation from. I guess that since there are two $T_1$ tensions on the right side of the middle pulley, then the second tension must be half $T_1$?

Yes, this is the FBD of the middle pulley. An ideal (massless pulley) has the force equation $F = ma = 0 = T_2 - 2T_1$.

 

[Davidllerenav]

Yes, this is the FBD of the middle pulley. An ideal (massless pulley) has the force equation $F = ma = 0 = T_2 - 2T_1$.

I didn't knew that. So everytime I have a massless pulley I can assume that?

 

[Orodruin]

ecwrytumw

I think you need to double check the placement of your fingers on the keyboard ...
But yes. Any time you have an ideal massless object, the forces acting on it need to cancel out.

 

[Davidllerenav]

I think you need to double check the placement of your fingers on the keyboard ...
But yes. Any time you have an ideal massless object, the forces acting on it need to cancel out.

Sorry, I'm from my cellphone and didn't notice. I meant "everytime". So the forces cancel and the tensions also have that relationship?

 

[haruspex]

and the tensions also have that relationship?

The forces and torques cancel, so they may have a relationship, but not necessarily that one, exactly.
The right-hand pulley is on a bracket, so the tensions balance the force from that. The left-hand pulley is only in contact with the strings, so the forces from the tensions must balance somehow. All the strings are parallel, so it's easy, but in another problem the string that runs around the pulley might go off at some angle.