Pytels Dynamics 12.10: parabolic path, velocity, acceleration

[Alexanddros81]

Homework Statement

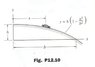
An automobile goes down a hill that has the parabolic cross section shown. (see image attached)
Assuming that the horizontal component of the velocity vector has a constant
magnitude v₀, determine (a) the expression for the speed of the automobile in
terms of x; and (b) the magnitude and direction of the acceleration.

Homework Equations

y=h(1-x²/b²)

The Attempt at a Solution

I have attached an image

It gives a solution in (a) v₀√1+(2hx/b²)²
and (b) 2hv₀²/b²

How do I proceed in (a) to come to the given solution?

 

[kuruman]

Have you considered mechanical energy conservation?

 

[Alexanddros81]

Conservation of mechanical energy is introduced later in pages 148-149.
This problem is at the first pages(pg. 23) of Dynamics 2nd edition under the Rectangular Coordinates section.

 

[kuruman]

Actually, I was off the mark initially. This is not an energy conservation problem, but a simple application of calculus. You are looking for $v = \sqrt{v_x^2+v_y^2}$. You know that $v_x = v_0$, that $y = h(1-x^2/b^2)$ and that $v_y = dy/dt$. So ...

 

[Alexanddros81]

so for v_y = dy/dt i get v_y = - (h/b²)2x

and v = sqrt(v₀² + (- (h/b²)2x)²)

I don't know how to proceed then

 

[kuruman]

so for v_y = dy/dt i get v_y = - (h/b²)2x

You did not apply the chain rule of differentiation carefully enough. Try again. Remember that x depends on time.

 

[Alexanddros81]

Ok. What I get is different from the given soution at the back of the book.
It is given $v = v_0 \sqrt {1 + \left( \frac {2hx} {b^2}\right) ^2}$
what I get is $v = v_0 \sqrt {1 + \left( \frac {-2hx} {b^2}\right) ^2}$
Check also my upload

 

[kuruman]

$\left( -\frac{2hx}{b^2} \right)^2=\left( (-1)\frac{2hx}{b^2} \right)^2=(-1)^2\left( \frac{2hx}{b^2} \right)^2=\left( \frac{2hx}{b^2} \right)^2$

 

[Alexanddros81]

Any hint in finding the magnitude of acceleration?
It should be $\frac {2hv_0^2} {b^2}$

I have done the $a_y=\frac {d} {dt}\left( v_y\right) = \frac {d} {dt} \left [v_0\left(\frac {-2hx} {b^2}\right)\right]$. How do i proceed from here?

and $a_x$ should be zero since $v_x$ is constant

 

[ehild]

Any hint in finding the magnitude of acceleration?
It should be $\frac {2hv_0^2} {b^2}$

I have done the $a_y=\frac {d} {dt}\left( v_y\right) = \frac {d} {dt} \left [v_0\left(\frac {-2hx} {b^2}\right)\right]$. How do i proceed from here?

and $a_x$ should be zero since $v_x$ is constant

Apply Chain Rule, (see @kuruman's Post#6)

 

[Alexanddros81]

It should be as shown at the attached file