leolaw
- 85
- 1
You want to get an idea of the magnitude of magnetic fields produced by overhead power lines, You estimate that the two wires are each about 30m above the ground and are about 3m apart. The local power company tells you that the lines operate at 10kV and provide a maximum of 40MW to the local area. Estimate the maximum magnetic field you might experience walking under these power lines, and compare to the Earth's field. (For an ac current, values are rms, and the magnetic field will be changing)
I don't quite understand the problem but i believe that the maximum magnetic field is below and between the two wires. I also found the V_rms and I_rms.
V_{rms}=\frac{V_0}{\sqrt{2}}\\
V_{rms} = \frac{10kV}{\sqrt{2}}
V_{rms} = 7071.07V
{and}
P = V_{rms}*I_{rms}
40E6 = 7071.07 * I_{rms}
I_{rms} = 5656.85A
ANd i have no ideas what should i go next
I don't really get what does the change of the direction of the magnetic field have to do with the magnitude. Isnt that would be the same no matter what?
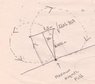
The attached image is what I am thinking right now
[edit] i will upload the image later, because i need to fix my scanner [/edit]
I don't quite understand the problem but i believe that the maximum magnetic field is below and between the two wires. I also found the V_rms and I_rms.
V_{rms}=\frac{V_0}{\sqrt{2}}\\
V_{rms} = \frac{10kV}{\sqrt{2}}
V_{rms} = 7071.07V
{and}
P = V_{rms}*I_{rms}
40E6 = 7071.07 * I_{rms}
I_{rms} = 5656.85A
ANd i have no ideas what should i go next
I don't really get what does the change of the direction of the magnetic field have to do with the magnitude. Isnt that would be the same no matter what?
The attached image is what I am thinking right now
[edit] i will upload the image later, because i need to fix my scanner [/edit]
Attachments
Last edited: