Shaybay92
- 122
- 0
So I have the following shape for which I want to calculate the inertia matrix. Basically I just want to know what limits of integration I should use if I am using spherical coordinates. Assume the convention that phi is the angle from x to y in the xy plane and theta is from z to the xy plane. Thus the limits I chose were [theta, -pi/2,pi/2] and [phi,0,pi/2]. Do you agree with these? The reason I ask is I am getting zero for my calculation of Izz.
Thanks in advance.
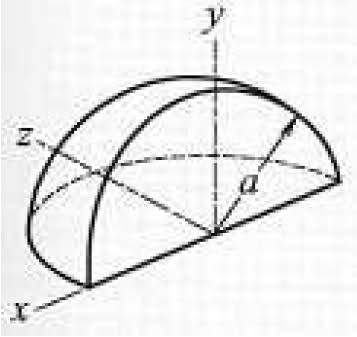
Thanks in advance.