- #1
meanswing
- 10
- 0
This is for question 7.53b) . I understand that the inductor acts like a short circuit but how is the current through the inductor affected? Wont the current source (6 A) split at the node before the 4 ohm resistor and before going into the 2 ohm resistor?
Also to get the Equivalent Resistor when the switch is open is troubling me? At first i wanted to add the 4ohm and 2ohm resistor since they are in series but my answer was wrong. The correct answer was 2ohm? Isnt the 4ohm and 2ohm resistor in series even though the switch is open?
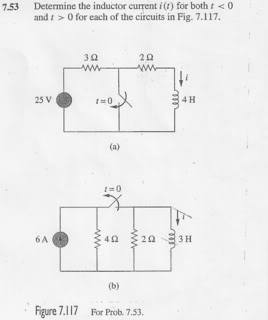
Also to get the Equivalent Resistor when the switch is open is troubling me? At first i wanted to add the 4ohm and 2ohm resistor since they are in series but my answer was wrong. The correct answer was 2ohm? Isnt the 4ohm and 2ohm resistor in series even though the switch is open?