Automated
- 3
- 0
"
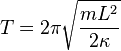
Solving this for κ, substituting into (1), and rearranging for G, the result is:
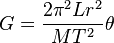 "
"
I am trying to rearrange the first equation to make κ the subject and I get:
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(6).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(5).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(4).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(3).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(2).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(1).gif[/URL]
But somehow I think I've done something wrong :S Please could someone point out where I've gone wrong (or if I am indeed actually right, then how I substitute it into
equation (1) which is [PLAIN]http://upload.wikimedia.org/math/2/c/a/2ca1bb59fb981ea80bd5c3d642d26949.png)
Thanks :)
Solving this for κ, substituting into (1), and rearranging for G, the result is:
I am trying to rearrange the first equation to make κ the subject and I get:
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(6).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(5).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(4).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(3).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(2).gif[/URL]
[URL]http://www.adamrapley.com/eqn1/CodeCogsEqn%20(1).gif[/URL]
But somehow I think I've done something wrong :S Please could someone point out where I've gone wrong (or if I am indeed actually right, then how I substitute it into
equation (1) which is [PLAIN]http://upload.wikimedia.org/math/2/c/a/2ca1bb59fb981ea80bd5c3d642d26949.png)
Thanks :)
Last edited by a moderator: