unscientific
- 1,728
- 13
Homework Statement
Homework Equations
The Attempt at a Solution
Is my initial assumption wrong?
unscientific said:Homework Statement
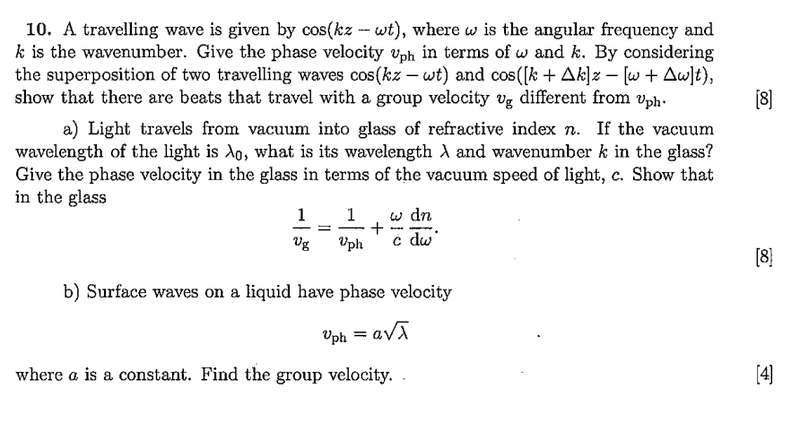
Homework Equations
The Attempt at a Solution
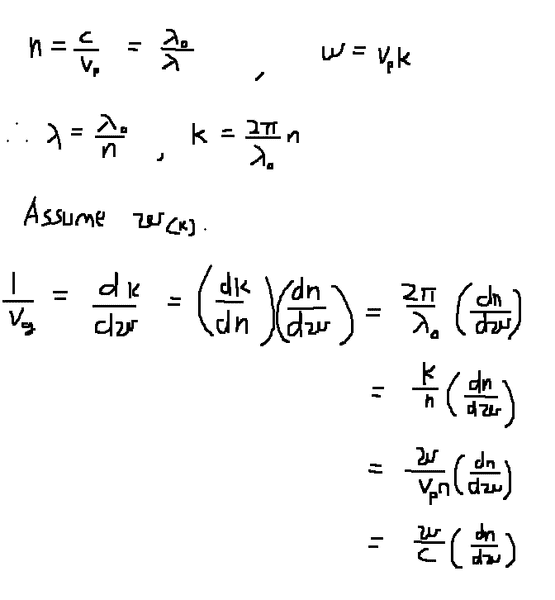
Is my initial assumption wrong?
rude man said:No, it's right.
unscientific said:But I seem to be missing out on a 1/vph term..