SmokeyMTNJim
- 18
- 0
Here is the problem: I have already lost the ability to get the correct answer for AI
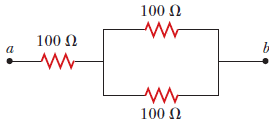
(a) What is the maximum potential difference that can be applied to the terminals a and b?
33.541

Which resistor will have the largest current? V
(b) For the voltage determined in part (a), what is the power delivered to each resistor?
resistor on the left W
resistor at the top of the loop W
resistor at the bottom of the loop W
(c) What is the total power delivered to the combination of resistors?
W
V=IR, P=IV, P=I^2R
Resistors in series = R+R+R...
Resistors in parallel (1/R)+(1/R)+(1/R)...[/B]
My thought process was: If the max power to anyone resistor could be 22.5 watts then use P=IV, substitute the V for V=IR.
My equation is now P=I^2R or 22.5W = I^2 (100Ω) => I = .4743 A for current at the resistor on side A. V=IR => V=.4743(100) => V=47.43
I tried a similar method for the other side after consolidating the Resistors 1/100 + 1/100 = .2 => 1/.2 = 50. Basically a------100Ω--------50Ω--------b
No dang just thought to add these to together and get a Reqiv. for the whole thing. So i just used the same method of P=I^2R to get a I = .3873.
V=IR => 150Ω(.3873) = 58.095 V << Is this what you would get for part a? I don't really want to plug in answers yet for the problem if its wrong
Homework Statement
(a) What is the maximum potential difference that can be applied to the terminals a and b?
33.541
Which resistor will have the largest current? V
(b) For the voltage determined in part (a), what is the power delivered to each resistor?
resistor on the left W
resistor at the top of the loop W
resistor at the bottom of the loop W
(c) What is the total power delivered to the combination of resistors?
W
Homework Equations
:V=IR, P=IV, P=I^2R
Resistors in series = R+R+R...
Resistors in parallel (1/R)+(1/R)+(1/R)...[/B]
The Attempt at a Solution
My thought process was: If the max power to anyone resistor could be 22.5 watts then use P=IV, substitute the V for V=IR.
My equation is now P=I^2R or 22.5W = I^2 (100Ω) => I = .4743 A for current at the resistor on side A. V=IR => V=.4743(100) => V=47.43
I tried a similar method for the other side after consolidating the Resistors 1/100 + 1/100 = .2 => 1/.2 = 50. Basically a------100Ω--------50Ω--------b
No dang just thought to add these to together and get a Reqiv. for the whole thing. So i just used the same method of P=I^2R to get a I = .3873.
V=IR => 150Ω(.3873) = 58.095 V << Is this what you would get for part a? I don't really want to plug in answers yet for the problem if its wrong