Jonnyto
- 12
- 0
Homework Statement
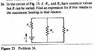
In the circuit of Fig. 23, ℰ, R1, and R2 have constant values but R can be varied. Find an expression for R that results in the maximum heating in that resistor.
Homework Equations
V=IR
resistors in parallel add up in inverse,
resistors in series add up directly,
The Attempt at a Solution
Okay so the way I undertook this problem was considering as R2 and R to be parallel, so I found the equivalent capacitance of those two. I got that new resistance and and then I considered R1 and then the new parallel system of parallels to be resistors in series. Later I used Kirchoff's Loop rule to isolate the new capacitance. ε-iReq=0
I used basic algebra to separate the R from all other values. Was this correct? I left the current, i, in the expression. The current is not actually part of the given.