Engr.abshir
- 5
- 0
Homework Statement
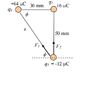
A 64 microC charge is locate 30 cm to the left of a 16 micro C charge. What is the resultant force
on a -12 micro C charge positioned exactly 50 mm below the 16 micro C charge?
Homework Equations
coulomb law f=k*qq/(r^2),resultant force,resolve into x and y component.
The Attempt at a Solution
the first three steps are straightforward
first step
using Pythagoras rule gives s=58.3 mm and theta = 59.0 degree
the force b/w q1 and q2 using coulomb law i calculated
F13 = 2033 N.
similarly ,the force between q2 and q3, gives correctly
F 23= 691 N.
i am having trouble understanding these steps about resolving it into components.i need some revision here.
Fx = 0- F13 cos 59.0 (where does the zero come from?)
= -(2033 N) cos 59.0
which gives Fx = -1047 N
also
Fy = F23 + F13 sin 59.00(why add force 23)
= 691 N + (2033 N) sin 590
Fy = 2434 N
i can do the rest.
Attachments
Last edited: