antsknee
- 6
- 0
Hi,
I am trying to work out the resonant frequency of an annular ring, does anyone know a general equation for it?
For example the ring has an outside diameter = OD and inside diameter = ID. The ring is gently clamped at the outside diameter and a force F applied evenly at the inside diameter. At a particular frequency the amplitude of displacement will be maximum.
I believe it would be something like hookes law. The thickness of the ring would be a factor as well as the elastic modulus of the ring.
Thanks,
Anthony.
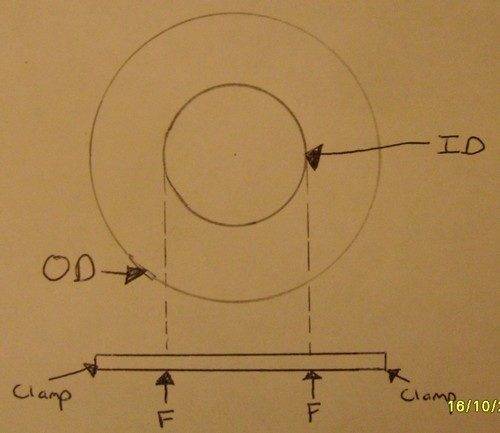
I am trying to work out the resonant frequency of an annular ring, does anyone know a general equation for it?
For example the ring has an outside diameter = OD and inside diameter = ID. The ring is gently clamped at the outside diameter and a force F applied evenly at the inside diameter. At a particular frequency the amplitude of displacement will be maximum.
I believe it would be something like hookes law. The thickness of the ring would be a factor as well as the elastic modulus of the ring.
Thanks,
Anthony.
