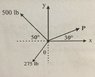
If you take the original force diagram and decompose the vectors shown into components, you should obtain two equations in P and θ. You know the x-component of the resultant is equal to 0, while the y-component must equal 425 lbs. Further algebraic manipulation yields and equation in sin θ and another in cos θ. By squaring and adding these two equations together, one can use the Pythagorean relation to eliminate θ, leaving a quadratic in P, which of course gives two values as solutions.
By substituting these values of P back into one of the earlier equations involving θ, you can obtain a pair of angles which are also solutions, but only one angle will work with a given solution to P, while the other angle works with the other solution to P. This is why there are four answers given.
Now, instead of dancing around this problem, if you would like to share your work towards solution, we may be able to see where you went wrong in your original attempt.
 ... fixed
... fixed
