Emperor42
- 15
- 0
If you have an optics system where you know the spot diagram of the image at on imaging on one plain and projecting onto another. Where you know the spot size for a point source at a given distance from the centre of the field.
Now if you reverse the system where the imaging plain now becomes the object plain and vice versa, can you extrapolate the new spot sizes from the old ones? Does it depend on the magnification?
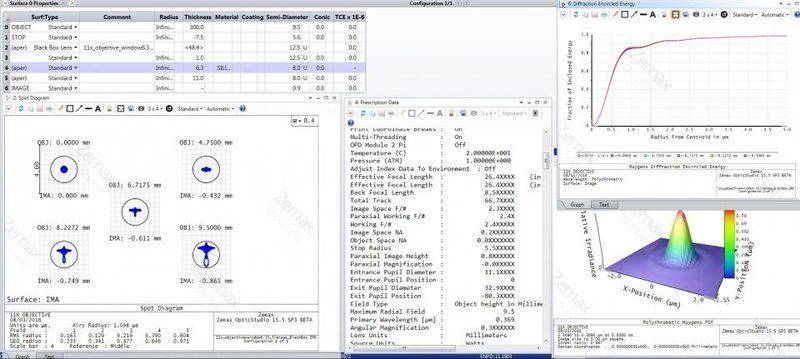
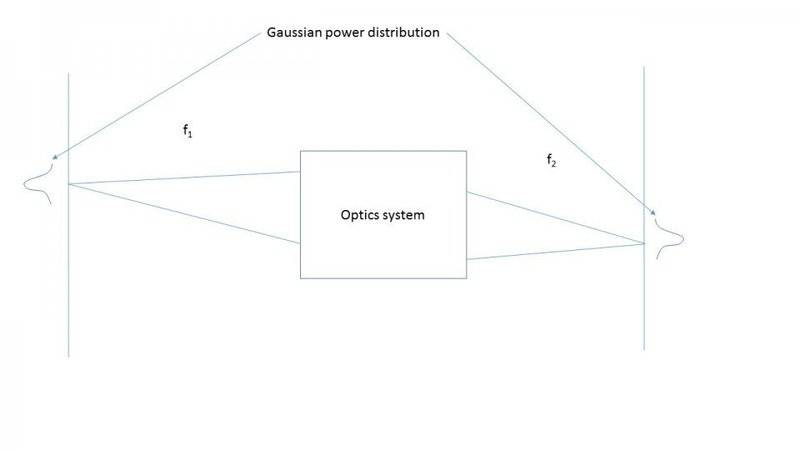
Now if you reverse the system where the imaging plain now becomes the object plain and vice versa, can you extrapolate the new spot sizes from the old ones? Does it depend on the magnification?