Ring moving along frictionless arc

AI Thread Summary
The problem involves a 5 kg ring sliding along a frictionless arc with a radius of 1.2 meters, influenced by two forces: a 40N tangential force and a 150N force at a 30-degree angle above the horizon. To calculate the total work done by these forces as the ring moves from points A to B and A to C, one must determine the components of the forces acting parallel to the arc length. The arc length from A to B is given as 1.88 meters. The discussion highlights the need to apply the work formula W = F x D while considering the effective force components along the arc.
fyonatan
Messages
2
Reaction score
0

Homework Statement



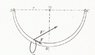
The ring (m), which weighs 5Kg, is sliding along a frictionless arc (Shown in the draw).
Arc radius - 1.2 meters.
There are 2 forces applied on the ring:
1) F - 40N and always tangent to the circle.
2) F' - 150N, 30 degrees above the horizon.

Calculate the total Work of the two forces when the body is sliding from A to B, and A to C.

Homework Equations





The Attempt at a Solution

 

Attachments

  • SCAN0130.JPG
    SCAN0130.JPG
    19.8 KB · Views: 461
Physics news on Phys.org
What is work defined as? How can you get the component of the force that is working parallel to the arc length? What is the arc length between A and B, B and C? Show some work?
 
The work is defined by W= F x D.

The Arc's length between A to B is 1.88 meters.

I really don't know where to start.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Frictionless ring sliding on circle in constant acceleration
Replies
16
Views
2K
Solving a Simple Diff. Eq: Block in a Frictionless Ring
Replies
10
Views
2K
Where is wrong in this proof for rotational inertia ?
Replies
8
Views
2K
Solving a Friction-Constrained Motion Problem
Replies
7
Views
2K
Electric Field from Arc of Charge - Need Help
Replies
19
Views
28K
Find the speed of the descending block
Replies
7
Views
2K
Work of gravity on an object sliding down a frictionless sphere
Replies
12
Views
2K
Find Velocity and Position of Mass on Frictionless Table
Replies
15
Views
3K
Three charges constrained to a ring
Replies
4
Views
1K
A mass is free to move on a horizontal frictionless surface
Replies
10
Views
6K

Hot Threads

Recent Insights

Back
Top