How Is the Speed of Contact Point B Calculated in Rod and Block Dynamics?

[Saitama]

Homework Statement

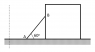
Rod AB is placed against a block which is moving towards right with a speed of 1m/s. If at an instant when the rod makes an angle $60^{\circ}$ with the horizontal and end A is sliding towards left with a speed of 1m/s. Then the speed of the point of contact B of the rod is?

(Ans: $\sqrt{3}/2\,\,\text{m/s}$)

Homework Equations

The Attempt at a Solution

Let the horizontal distance from the dashed line of point A be $x_A$ and that of B be $x_B$. Also, let the distance of B from ground be $y$. Clearly, $dx_A/dt=-1\,\,\text{m/s}$ and $dx_B/dt=1\,\,\text{m/s}$. From Pythagoras theorem,

$$(x_B-x_A)^2+y^2=l^2 \Rightarrow 2(x_B-x_A)\left(\frac{dx_B}{dt}-\frac{dx_A}{dt}\right)+2y\frac{dy}{dt}=0$$
where $l$ is the length of rod.
$$\Rightarrow -y\frac{dy}{dt}=2(x_B-x_A) \Rightarrow \frac{dy}{dt}=-\frac{2}{\sqrt{3}}\,\,\text{m/s}$$
where I have used $\tan(60^{\circ})=y/(x_B-x_A)=\sqrt{3}$.

Hence, the net velocity is
$$\sqrt{1^2+\left(-\frac{2}{\sqrt{3}}\right)^2}=\sqrt{\frac{7}{3}}\,\,\text{m/s}$$

Where did I go wrong?

Any help is appreciated. Thanks!

 

[Tanya Sharma]

Hi Pranav...

Your work looks alright to me .

 

[I like Serena]

Hey Pranav!

Can it be they wanted to know the speed of point B relative to the block?
And furthermore that in the given answer the numerator and denominator are swapped around?

 

[Saitama]

Hi Pranav...

Your work looks alright to me .

Hi Tanya! :)

I too feel that there is nothing wrong with my work but then I don't see what's wrong with the given solution to this problem. I have attached the solution.

Hey Pranav!

Can it be they wanted to know the speed of point B relative to the block?
And furthermore that in the given answer the numerator and denominator are swapped around?

Hi ILS!

I copied the problem word by word. I have attached the solution given and I can't follow what's going on in the solution. It looks as if they are equating the component of velocity along the rod. Please have a look. :)

 

[Tanya Sharma]

Hi Tanya! :)
I too feel that there is nothing wrong with my work but then I don't see what's wrong with the given solution to this problem. I have attached the solution.

The solution is simply wrong for the reason that 1/2 m/s may be the component of velocity of tip B along the rod ,but it is surely not the velocity of the tip with respect to the block .

v_B = v_B,Block + v_Block

Does this makes sense ?

 

[Saitama]

The solution is simply wrong for the reason that 1/2 m/s may be the component of velocity of tip B along the rod ,but it is surely not the velocity of the tip with respect to the block .

v_B = v_B,Block + v_Block

Does this makes sense ?

Umm...why do we talk about the velocity with respect to block?

 

[I like Serena]

Hi ILS!

I copied the problem word by word. I have attached the solution given and I can't follow what's going on in the solution. It looks as if they are equating the component of velocity along the rod. Please have a look. :)

Interesting.

With their speed along the bar, point B would become detached from the block since its horizontal speed would exceed 1 m/s.
But if that is supposed to be the case, we do not have enough information, and the problem does refer to "the point of contact B".

Anyway, I don't understand either why they would take the component of the velocity at A along the rod.
And I certainly do not understand how they added the two velocities at point B - they appeared to have applied the cosine rule the wrong way.

I'd stick with your solution.
As an alternative and a verification, you can look at a frame that moves with point A.
In that frame the horizontal speed at point B is 2 m/s and point A is fixed.
Then it follows immediately that the vertical speed at point B has to be 2/√3.

 

[Saitama]

I'd stick with your solution.
As an alternative and a verification, you can look at a frame that moves with point A.
In that frame the horizontal speed at point B is 2 m/s and point A is fixed.
Then it follows immediately that the vertical speed at point B has to be 2/√3.

Yes, I tried that frame when Tanya talked about velocity with respect to block and I get the same answer. :)

But why do you say it exceeds 1m/s? I think the horizontal velocity would become less than 1 m/s that's why it detaches, right?

And the sad part is, I lost 4 marks. :(

 

[Tanya Sharma]

Decompose the velocity vector into any two perpendicular directions x and y, say v=v_x+v_y .

Again decompose the velocity vector into another set of perpendicular direction m and n ,say v=v_m+v_n .

Do you think v=v_x+v_m ?

The problem with the solution is that they are combining components of velocity in different sets of perpendicular directions .If they wanted to use velocity of tip B along the rod then they should have combined that with the component perpendicular to the rod .

 

[I like Serena]

But why do you say it exceeds 1m/s? I think the horizontal velocity would become less than 1 m/s that's why it detaches, right?

And the sad part is, I lost 4 marks. :(

You're quite right. It's less than 1 m/s.
Perhaps you can get your points back if you ask for them.

 

[Saitama]

Decompose the velocity vector into any two perpendicular directions x and y, say v=v_x+v_y .

Again decompose the velocity vector into another set of perpendicular direction m and n ,say v=v_m+v_n .

Do you think v=v_x+v_m ?

The problem with the solution is that they are combining components of velocity in different sets of perpendicular directions .If they wanted to use velocity of tip B along the rod then they should have combined that with the component perpendicular to the rod .

Agreed, thanks a lot Tanya!

Perhaps you can get your points back if you ask for them.

If the results are not declared by tomorrow, I can ask them to do the corrections. :)

 

[haruspex]

The problem with the solution is that they are combining components of velocity in different sets of perpendicular directions .If they wanted to use velocity of tip B along the rod then they should have combined that with the component perpendicular to the rod .

Maybe it comes to the same thing, but I would characterise the blunder a little differently. Looks to me like they took the 0.5 m/s along the rod as a component velocity to be added to the horizontal velocity. Instead, it is a component of the resultant velocity (of the horizontal and vertical movements). If the vertical velocity is u and the overall velocity v we have v² = u² + 1, and resolving along the rod: u sin 60 - 1 cos 60 = 0.5.