tater08
- 29
- 0
Homework Statement
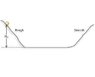
A basketball (which can be closely modeled as a hollow spherical shell) rolls down a mountainside into a valley and then up the opposite side, starting from rest at a height H0 above the bottom. In the figure, the rough part of the terrain prevents slipping while the smooth part has no friction.
How high, in terms of H0, will it go up the other side?
Homework Equations
THe KE of a thin hollow sphere is (2/3 mr^2)v^2 but i do not need it here
The Attempt at a Solution
i guess i just need a push into the right direction. I assuming that the terms of the ball reaching the height on the other side will have to do something of its circumference.